이전에 포스팅에서도 봤듯이, 적절한 회귀 계수를 가지는 것이 매우 중요하다. 회귀 계수가 너무 낮다면,
데이터들을 충분히 표현하지 못하는 회귀선이 만들어지게 되고, 회귀 계수가 지나치게 높다면,
학습 데이터에만 너무 치중이 되어 과적합 문제를 일으킨다.
그렇다면, 적절한 회귀 계수를 어떻게 찾을 수 있을까?
그렇다면, 어느 회귀선이 데이터를 가장 '적절하게' 표현하는 지에 대한 기준이 명확하게 존재해야 한다.
하지만, 일반적인 통념에 의존하여 우리는 '적절하다'를 표현하고, 어느 회귀선이 다른 회귀선들보다
절대적으로 더 낫다.라는 개념은 없다. 그렇기 때문에, 우리는 '적절한' 회귀선을 찾을 수 있는 방안에 대해서
여러가지(여기에서는 3가지 - 릿지, 라쏘, 엘라스틱넷)가 존재하는 것이다.
다시 앞으로 돌아가서 기존에 회귀선을 평가하는 방법에 대해서 알아보자.
우리는 오차들을 제곱해서 모두 더한 값들의 수치를 비교하여, 회귀선을 평가했다. 하지만, 이렇게 되면 위에서도 언급한 것처럼 모델이 회귀 계수를 무한정으로 높여, 학습데이터와의 오차가 0으로 수렴하도록 만드는 것에만 초점을 두어 학습할 수 있다. 이런 경우에 과적합 문제가 많이 발생한다. 따라서 이후에 사람들은 회귀 계수의 값들을 비용함수에
더해서 회귀 계수의 크기나 개수도 제한이 되도록 만들었다.
결과적으로 비용함수는
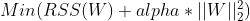
가 된다.
그 중에 L1, L2가 있는데, L2는 릿지회귀 , L1을 라쏘회귀라고 부른다.
(L1회귀는 ||W||_2^2 대신에 ||W||_1이며, alpha를 조절하는 것이 규제이다.)
위에서 얘기한것 처럼 alpha를 조절하면서 회귀 계수가 너무 커지는 것을 막거나, 회귀 계수의 값을 작게한다.
alpha를 증가시키면, W의 값이 커지는 것에 대해서 비용함수의 증감이 큰 폭으로 변할 것이다.
alpha를 감소시키면, W의 값의 변동에 따라 비용함수의 증감이 더 적은 폭으로 변하게 될 것이다.
릿지회귀
릿지회귀는 L2회귀라고도 부르며,

로 표현한다.
이렇게 표현하는 이유는, 비용함수를 계산할 때, 단순히 오차의 값을 더하는 것이 아닌, 오차의 제곱들을 합한것 처럼, 회귀 계수를 이용하는 경우에도 동일하게 사용한다. 제곱의 합을 더함으로써, 기존의 값을 더하거나, 기존의 값에 절댓값들을 더한것보다도, 비용함수가 W의 영향을 더 많이 받게된다. 이런 원리로, 릿지 회귀는 회귀 계수의 크기를 비교적 많이 감소시킨다.
라쏘 회귀
라쏘회귀는 L1회귀라고 부른다. 라쏘 회귀는 계수들의 값의 절댓값들을 더한 것으로 비용함수를 계산한다. 이렇게 함으로써, 릿지 회귀처럼, 전반적인 모든 계수들의 크기를 감소시키는 것보다는, 불필요한 계수의 값을 아예 0에 가깝게 만들어서 마치 해당 계수가 제거된 것처럼 만든다. 이런 면에서 L1 규제는 적절한 피처만 회귀에 포함시키는 피처 선택의 특성을 가지고 있다고 볼 수 있다.

엘라스틱넷 회귀
이 회귀는 L2규제(릿지 회귀)와 L1규제(라쏘 회귀)를 결합한 회귀이다. 비용함수는
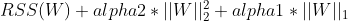
이고, 이 식을 최소화하는 W를 찾는 것이 목표이다.
이렇게 두 규제를 혼용하는 것에 대한 장점은 라쏘 회귀의 단점을 보완한다는 측면에서 알아볼 수 있다. 위에서 언급한 것 처럼, 라쏘 회귀는 주요한 피처를 제외하고, 나머지 피처의 계수를 0으로 만드려는 성향이 있다. 이렇게 학습하는 과정에서 회귀 계수의 값이 급격하게 변동을 하는데, 이것을 릿지 회귀인 L2규제를 같이 사용함으로써 보완할 수 있다.
하지만, 식의 길이에서도 볼 수 있듯이, 계산할 양이 상대적으로 더 많아, 학습에 많은 시간이 걸린다.
'기계학습 > Machine Learning' 카테고리의 다른 글
| [파이썬 머신러닝 완벽 가이드] 회귀 실습(기본) - 자전거 대여 수요 예측 (0) | 2021.07.09 |
|---|---|
| [파이썬 머신러닝 완벽 가이드] 전처리, 로지스틱 회귀, 회귀 트리 (0) | 2021.07.08 |
| [파이썬 머신러닝 완벽 가이드] : 다항 회귀 ( Polynomial, 편향, 분산) (0) | 2020.09.02 |
| [파이썬 머신러닝 완벽 가이드] : 회귀 ( 선형 회귀 / 경사하강법) (0) | 2020.08.30 |
| [파이썬 머신러닝 완벽가이드] : 사이킷 런 앙상블 러닝 ( Stacking ) (0) | 2020.08.25 |

최근댓글