본격적으로 시계열 분석에 들어가기 전에 기본적인 데이터 분석의 진행 방향에 대해서 먼저 다뤄보자.
이상적인 데이터 분석 단계
1. 데이터 수집
2. 데이터 전처리
3. 데이터 정리
4. 데이터 분석
5. 결과 정리
하지만, 현실적인 데이터 분석의 과정에서는 이 과정들이 칼로 벤 것처럼 딱 맞아 떨어지지 않는다!
데이터 분석

1단계
문제를 정의하는 단계
- 무엇을 예측할 것인가?
(ex> 직원들의 퇴사율)
- 필요한 데이터는 어떤 것인가?
(ex> 직원들이 의자에서 일어나는 횟수, 화장실 가는 빈도 등)
- 각 상태를 나타내는 기준은 어떻게 정할 것인가?
2단계
통상적으로 현재 우리가 집중적으로 공부하고 있는 분야
- 데이터 전처리
- 최적의 알고리즘 선정
- 선정한 알고리즘에 전처리한 데이터 입력 및 결과 반환
3단계
알고리즘의 결과를 해석하는 단계
- 결과를 어디에 어떻게 적용할 것인가?
- 실질적으로 효과가 있는 결론인가?
실무 측면에서 프로젝트 진행 방향
0. 문제 정의
1. 데이터 수집 : 소스별 데이터 수집 및 저장
2. 데이터 전처리 : 기초 통계 + 데이터 추가 및 삭제
3. 데이터 정리 : 데이터 통합 및 분리
4. 데이터 분석 : 기초 통계 + 모델링 + 검증지표 + 잔차진단
5. 결과 정리 : 시각화 + 의사결정 + 지식화 + 공유(발표)
★ 0 ~ 4 단계를 지속적으로 반복하고 업데이트하며 인사이트를 찾아낸다.
통계를 사용할 때에 주의 사항
- 무조건 통계에 의존하는 것은 안된다!
- 통계는 가능성을 보여주는 것이지 결과를 보장해주는 것이 아니다.
- 기본적으로 가정에 어느정도의 오류가 존재하고 있음을 인지해야 한다.
(가설 검정이 완벽하게 들어맞는 환경을 만들기는 거의 불가능에 가깝다.
- 통계에 무조건적으로 의존하기 보다는 객관적인 근거를 늘려나간다는 식으로 이용해야 한다.
수학, 통계 용어 정리
데이터 종류
| 데이터 종류 | 특징 | 설명 |
| 횡단면 데이터 | 특정 시점, 多 독립변수 | 시계열이 아닌 일반 데이터 |
| 시계열 데이터 | 다수 시점, 특정 독립 변수 | 한가지 특성의 시간에 따른 변화를 기록한 데이터 |
| 시계열 횡단면 데이터 | 다수 시점, 多 독립변수 | 복수개의 특성들이 각각 임의의 시간대의 기록을 가지고 있는 데이터 가장 일반적인 시계열 데이터 |
| 패널 데이터 | 다수 시점, 多 독립변수 | 복수개의 특성들이 같은 시간대의 기록을 가지고 있는 데이터 가장 이상적인 시계열 데이터 |
X를 나타내는 용어
- 독립 변수
- 설명 변수
- column, features,...
Y를 나타내는 용어
- 종속 변수
- Target
- Label Data...
통계 기본 용어
- 중심 통계량 :
- 평균(Average) : 전체 데이터의 합을 데이터의 개수로 나눈 값
- 중앙값(Median) : 전체 데이터에서 가운데에 위치하는 값
- 최빈값(Mode) : 전체 데이터에서 가장 많이 등장하는 값
- 변동 통계량 :
- 범위(Range) : 최댓값과 최솟값을 양 끝으로 하는 구간
- 편차(Deviation) : 평균과 관측값의 차이
- 변동(Variation) : 편차 제곱의 합
- 형태 통계량 :
- 왜도(Skewness) : 평균을 중심으로 편향된 정도
음수 - 왼쪽 부분에 긴 꼬리, 중앙값을 포함한 자료가 오른쪽에 다수 분포
양수 - 오른쪽 부분에 긴 꼬리, 중앙값을 포함한 자료가 왼쪽에 다수 분포 - 첨도(Kurtosis) : 중심이 뾰족한 정도
기본 정의는 첨도값이 3일 때 정규분포와 동일한 형태라고 설명이 나와있다.(위키 백과)
편의상 해당 첨도 값에서 3을 뺴서 0일 때 정규 분포를 따른다고 가정하는 경우가 많다.
음수 - 정규분포보다 긴 꼬리, 중앙 부분에 덜 집중되어 뾰족한 모양
양수 - 정규분포보다 짧은 꼬리, 중앙 부분이 완만한 모양
- 왜도(Skewness) : 평균을 중심으로 편향된 정도
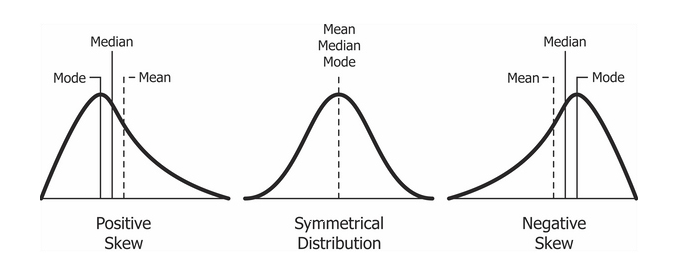
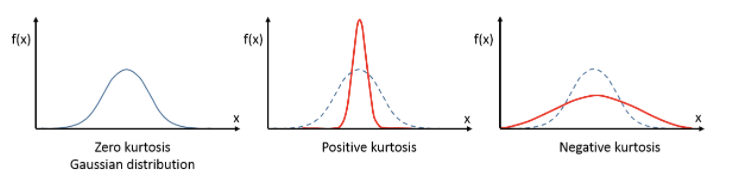
(출처 : https://brunch.co.kr/@data/13)
Reference :
패스트 캠퍼스 파이썬을 활용한 시계열 분석 A-Z
'딥러닝 > 시계열' 카테고리의 다른 글
| 시계열 분석 실습 코드 - 3 (0) | 2021.02.18 |
|---|---|
| 시계열 데이터 분석 코드 - 2 (0) | 2021.02.17 |
| 시계열 데이터 분석 실습 코드 - 1 (0) | 2021.02.16 |
| 시계열 데이터 분리, 분석 성능 확인 (검증지표, 잔차진단) (0) | 2021.02.16 |
| 시계열 데이터 패턴 추출 (Feature Engineering) 1 (3) | 2021.02.01 |

최근댓글