모델 선택과 평가, 교차 검증
파이프라인(pipeline), 특성 스케일링(feature scaling), fit, transform, fit_transform() 메서드의 차이 데이터 변환기, Pipeline 만들기 계층적 샘플링 (Stratified Sampling) 데이터 셋이 충분히 크다면 일반..
dsbook.tistory.com
가능성 있는 모델들을 모두 추렸다고 가정한 후, 이제 이 모델들을 세부 튜닝하기 위한 방법을 몇 가지 살펴보자.
하이퍼 파라미터 튜닝
1. GridSearchCV (그리드 탐색)
가장 단순한 방법은 만족할 만한 하이퍼 파라미터 조합을 찾을 때까지 수동으로 하이퍼 파라미터를 조정하는 것이다. 이는 매우 지루한 작업이고 또 많은 경우의 수를 탐색하기에는 시간이 부족할 수도 있다. 따라서 이를 대신하기 위해 사이킷런에서는 GridSearchCV 클래스를 제공한다. 탐색하고자 하는 하이퍼 파라미터와 시도해볼 값을 지정한 후 가능한 모든 하이퍼 파라미터 조합에 대해 교차 검증을 진행하여 평가하게 된다.
서포트 벡터 머신 회귀(sklearn.svm.SVR)를 모델로 선택했다고 가정하자. kernel="linear"일 때는 하이퍼 파라미터 "C"를 바꿔가면서, kernel="rbf"일 때는 하이퍼 파라미터 "C"와 "gamma"를 바꿔가면서 최상의 SVR 모델을 찾아보자. 지금 이 커널과 하이퍼 파라미터가 무엇을 뜻하는지는 너무 신경 쓰지 말자.
from sklearn.svm import SVR
from sklearn.model_selection import GridSearchCV
param_grid = [
{'kernel': ['linear'], 'C': [10., 30., 100., 300., 1000., 3000., 10000., 30000.0]},
{'kernel': ['rbf'], 'C': [1.0, 3.0, 10., 30., 100., 300., 1000.0],
'gamma': [0.01, 0.03, 0.1, 0.3, 1.0, 3.0]},
]
svm_reg = SVR()
# GridSearchCV(모델명, 하이퍼 파라미터 값(dict), cv=폴드 수, scoring=평가 방법, verbose=진행 상황 표시
grid_search = GridSearchCV(svm_reg, param_grid, cv=5, scoring="neg_mean_squared_error", verbose=2)
grid_search.fit(housing_prepared, housing_label)


실제로 kernel = "linear"일 경우 가능한 하이퍼 파라미터 조합은 8개, kernel = "rbf"일 경우 가능한 하이퍼 파라미터 조합은 42개, 총 50개의 하이퍼 파라미터 조합을 5번의 교차검증으로, 즉 250번 평가한다는 뜻이다. 각각의 파라미터에 대한 세부적인 결과는 GridSearchCV객체인 grid_search의 cv_results_ 속성을 통해 확인해볼 수 있으며 best_params_를 통해 최적의 파라미터 조합을 찾을 수 있다.
grid_search.best_params_
negative_mse = grid_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse
2. RandomizedSearchCV (랜덤 탐색)
그리드 탐색 방법은 이전 예제에서처럼 비교적 적은 수의 조합을 탐구할 때 괜찮다. 하지만 하이퍼 파라미터 탐색 공간이 커지면 RandomizedSearchCV를 사용하는 편이 더 좋다. 그리드 탐색과 거의 같은 방식으로 가능한 모든 조합을 시도하지만 각 반복마다 하이퍼 파라미터에 임의의 수를 대신 대입하여 지정한 횟수만큼 평가를 한다. 이 방법을 사용하여 내가 원하는 횟수만큼 최적의 하이퍼 파라미터 값을 찾을 수 있고, 이 반복 횟수를 조절하는 것만으로도 하이퍼 파라미터 탐색에 투입할 컴퓨팅 자원을 제어할 수 있다.
앞서 사용한 서포트 백터 머신 회귀 모델에서 그리드 탐색 방법 대신 랜덤 탐색 방법으로 하이퍼 파라미터를 튜닝해보자.
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import expon, reciprocal
# 이때 'kernel'이 'linear'일 경우 gamma값은 무시된다.
param_distribs = {
'kernel' : ['linear', 'rbf'],
'C' : reciprocal(20, 200000),
'gamma' : expon(scale=1.0),
}
svm_reg = SVR()
# RandomizedSearchCV(모델명, param_distributions=하이퍼 파라미터 조정 범위,
# n_iter="탐색 횟수", cv="폴드 수", scoring"=평가방법",
# verbose="진행 상황 표시", random_state="시드")
rnd_search = RandomizedSearchCV(svm_reg, param_distributions=param_distribs,
n_iter=50, cv=5, scoring="neg_mean_squared_error",
verbose=3, random_state=42)
rnd_search.fit(housing_prepared, housing_label)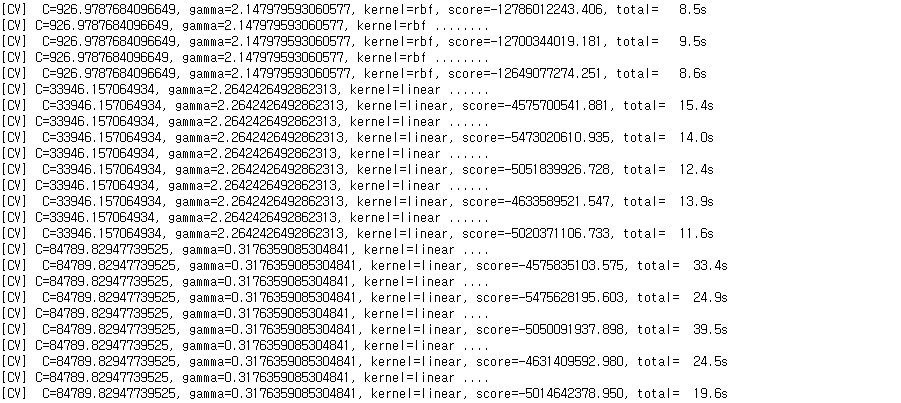


rnd_search.best_params_
negative_mse = rnd_search.best_score_
rmse = np.sqrt(-negative_mse)
rmse
실제로 탐색 횟수 50번, 그리고 각각의 탐색마다 5번씩 교차검증으로 평가하므로 총 250번 반복하게 된다.
테스트 세트로 시스템 평가하기
final_model = rnd_search.best_estimators_
X_test = strat_test_set.drop("median_house_value", axis=1)
y_test = strat_test_set["median_house_value"].copy()
X_test_prepared = full_pipeline.transform(X_test)
final_predictions = final_model.predict(X_test_prepared)
final_mse = mean_squared_error(y_test, final_predictions)
final_rmse = np.sqrt(final_mse)
final_rmse앞서 그리드 탐색 방법과 랜덤 탐색 방법으로 하이퍼 파라미터를 튜닝하는 과정에서 랜덤 탐색의 결과가 더 좋게 나왔으므로 랜덤 탐색에서 가장 좋은 성과를 낸 estiamtor를 통해 최종 모델을 결정지었다. 앞서 계층적 샘플링을 통해 나눈 테스트 세트에서 모델에 들어갈 데이터와 데이터 레이블을 다시 나눈다. 그 후 훈련 데이터 세트를 전 처리하기 위해 만들었던 파이프라인을 통해 테스트 세트가 모델에 들어가기에 알맞도록 변환시켜준다. 그렇게 준비한 최종 테스트 데이터 세트를 모델에 넣어 "중앙 주택 가격"을 예측하고, 준비된 레이블을 통해 모델을 평가한다.

이 추정값이 얼마나 정확한지 알아보고 싶다면 scipy.stats.t.interval()을 통해 일반화 오차의 95% 신뢰구간(confidence interval)을 계산할 수 있다.
from scipy import stats
confidence = 0.95
squared_errors = (final_predictions - y_test) ** 2
np.sqrt(stats.t.interval(confidence, len(squared_errors) - 1,
loc=squared_errors.mean(),
scale=stats.sem(squared_errors)))
Scipy.stats : Statistical function
1. reciprocal 함수
사이파이 모듈에서 통계적 함수를 담당하고 있는 API로 다양한 통계함수가 들어있다. scipy의 가장 최신버전인 1.5.1버전에서는 reciprocal 함수를 찾을 순 없지만 loguniform에서 그 함수를 찾을 수 있었다. (reciprocal = loguniform) reciprocal 함수는 a와 b를 인자로 가져 아래의 표준화된 형태의 확률 밀도 함수를 생성한다.
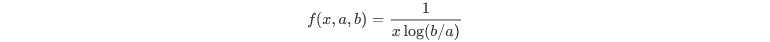
이 확률 분포 함수를 이동시키거나 스케일을 조정하려면 loc와 scale 파라미터를 조정해주면 된다. (보통은 loc=0, scale=1로 고정된다.) reciprocal의 다른 이름인 loguniform에서도 말해주 듯이, 이 확률 분포 함수를 로그화하였을 경우 주어진 범위 안에서 확률이 꽤 일정하게 나타난다. 아래에서 그 과정을 확인해 볼 수 있다.
reciprocal_distrib = reciprocal(20, 200000)
samples = reciprocal_distrib.rvs(10000, random_state=42)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.title("Reciprocal distribution (scale=1.0)")
plt.hist(samples, bins=50)
plt.subplot(122)
plt.title("Log of this distribution")
plt.hist(np.log(samples), bins=50)
plt.show()
2. expon 함수
expon 함수 역시 그 이름에서 알 수 있듯이 exponential, 즉 지수 분포 함수를 생성한다. 특별히 받는 인자는 없으며 아래의 표준화된 형태의 확률 밀도 함수를 생성한다.

이 함수 역시 이동하거나 스케일을 조정하고 싶을 때는 각각 loc과 scale 파라미터를 조정해주면 된다. (보통은 loc=0, scale=1로 고정된다.)
expon_distrib = expon(scale=1.)
samples = expon_distrib.rvs(10000, random_state=42)
plt.figure(figsize=(10, 4))
plt.subplot(121)
plt.title("Exponential distribution (scale=1.0)")
plt.hist(samples, bins=50)
plt.subplot(122)
plt.title("Log of this distribution")
plt.hist(np.log(samples), bins=50)
plt.show()
여기서 중요한 것은 reciprocal 분포함수는 우리가 하이퍼 파라미터에 대한 감이 전혀 없을 때, 즉 하이퍼 파라미터 값의 스케일을 어떻게 지정해야 할지 모를때 주로 사용하고, expon 분포함수는 하이퍼 파라미터 값의 스케일을 어느정도 알고있을 때 사용하는 것이 모델을 학습하는데 도움이 된다.
'기계학습 > Machine Learning' 카테고리의 다른 글
| [파이썬 머신러닝 완벽가이드] : 사이킷런 기본 - 1 (0) | 2020.07.29 |
|---|---|
| Machine Learning 의 개념 (0) | 2020.07.16 |
| [Hands-on Machine Learning] 모델 선택과 평가, 교차 검증 - housing data (0) | 2020.07.10 |
| [Hands-on Machine Learning] 파이프라인(pipeline), 특성 스케일링(feature scaling), fit, transform, fit_transform() 메서드의 차이 - housing data (0) | 2020.07.10 |
| [Hands-on Machine Learning] 계층적 샘플링 (Stratified Sampling) - housing data (0) | 2020.07.09 |

최근댓글