전 글에 이어서 진행됩니다.
원하는 데이터 값(들) 가져오기
인덱싱(원하는 요소 추출, 차원축소의 기능)
1차원 데이터에서 값 가져오기

numpy에서 인덱싱은 파이썬 리스트의 인덱싱과 비슷한 원리이다. [ ]를 사용하여 값을 추출해온고, 항상 첫 번째 값은 0부터 시작이다.
- 변수명[n] -> n+1번째 값을 가져온다.
- 변수명[-1] -> 마지막 값을 가져온다.
- 변수명[n] = 값 -> 원하는 위치에 값을 저장하여 데이터를 바꿀 수도 있다.
2차원 데이터에서 값 가져오기

2차원 데이터는 행과 열이 있느 데이터이다. (수학에서 x, y 좌표평면과 비슷한 개념이고 선형대수의 행렬이랑 같은 개념이다)
- 변수명[m, n] -> m+1번째 행, n+1번째 열을 가져온다. (마찬가지로 0부터 시작이여서 그렇다)
- 변수명[m] -> 이처럼 행과 열 값중 하나를 생략하고 전체를 다 가져올 수도 있다.
- 변수명[m, -1] -> -1을 사용하면 마지막 값을 가져올 수도 있다.
3차원 데이터에서 값 가져오기

3차원으로 이루어진 데이터들을 텐서라고 부른다. (수학에서 x, y, z축이 있는 것처럼 공간이라고 생각하면 편하다) 빠른 이해를 위해 행과 열로 이루어진 것들을 박스라고 부르겠다.
- 변수명[b, m, n] -> b+1번째 박스, m+1번째 행, n+1번째 열을 가져온다. (마찬가지로 0부터 시작이여서 그렇다)
슬라이싱(원하는 범위의 값들 가져오기, 차원유지)
1차원 데이터 원하는 값들 가져오기

numpy 슬라이싱은 python의 리스트 슬라이싱과 동일한 개념이다. 범위를 지정해 원하는 값을 가져올 때 많이 사용하고슬라이싱은 인덱싱과 다르게 차원을 유지하여 값을 가져온다. [ ] 대괄호 안에 : 기호를 사용해 , 콤마를 기준으로 가져온다.
- 변수명[a:b] -> a+1번째부터, b-1번째 값까지 가져온다.(항상 0부터 시작이고 b번째 값 이전(b-1)까지 가져온다)
2차원 데이터 원하는 값들 가져오기

- 변수명[a:b, c:d] ->a+1번째부터 b-1번째 행, c+1번째부터 d-1번째 열까지 값들을 가져온다.
- 변수명[ : , : ] -> 같이 숫자입력을 생략하고 전체를 다 가져올 수도 있다.
- 변수명[ , c:d ] -> 와 같은 형태 인덱싱과 혼합하여 값을 가져올 수도 있다.
3차원 데이터 원하는 값들 가져오기

- 변수명[a:b, c:d, e:f ] ->a+1번째부터 b-1번째 박스, c+1번째부터 d-1번째 행, e+1번째부터 f-1번째 열까지 값들을 가져온다.
- 변수명[ : , : , :] -> 같이 숫자입력을 생략하고 전체를 다 가져올 수도 있다.
- 변수명[ , a:b, c:d ] -> 와 같은 형태 인덱싱과 혼합하여 값을 가져올 수도 있다.
데이터 형태(차원, 배열) 변환하기
reshape함수(원하는 형태로 차원 변경)


n차원의 데이터가 있다고 가정하자. 내가 다른 차원의 데이터로 바꾸고 싶을 때, reshape 함수를 써 배열과 차원을 바꿀 수 있다. 단 주의해야 할 점은 바꿀려는 형태의 데이터 개수가 원래 데이터와 동일해야 한다.
ex) 20개가 있으면 (5 x 4), (2 x 2 x 5)와 같이 개수가 같아야 한다.
- 변수명.reshape(바꾸고 싶은 차원)
ravel함수, flatten함수(다차원배열을 1차원으로 변경)


ravel함수, flatten함수 둘 다 2,3,n차원 배열을 1차원의 데이터 형태로 나타내고 싶을 때 사용한다.
사용형태는 변수명.ravel() , np.ravel(변수명, order = ) 이고 flatten도 마찬가지다.
order= 'C'와 같이 값을 주면 행을 중심으로 변환하고, 'F'값을 주면 열을 중심으로 형태를 변환한다.
ravel함수 vs flatten함수 차이점 (값 저장의 유무)

ravel함수는 temp[0] = 100을 주고 x값을 출력했을 때, 100이 나옴을 볼 수 있다.
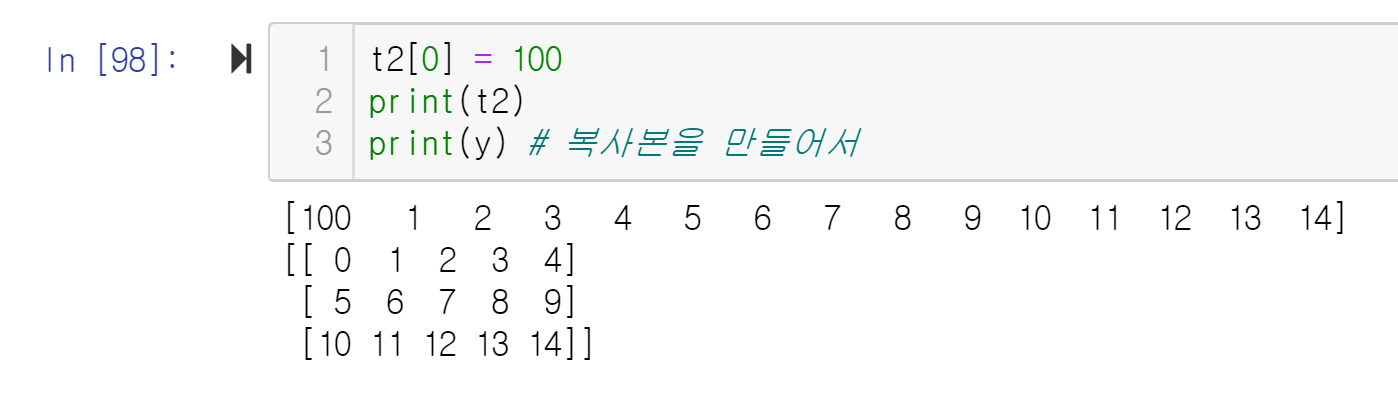
flatten함수는 t2[0] = 100을 주고 y값을 출력했을 때, 100이 아닌 원래 값 0이 나옴을 볼 수 있다.
이와 같인 두 함수의 차이점은 ravel함수는 원본 데이터를 그대로 저장해 사용하는 것이고, flatten함수는 복사본을 만들어 사용하는 것이다.
'데이터 사이언스 메뉴얼 > numpy' 카테고리의 다른 글
| (SM) 융합연구 - numpy모듈(4) [boolean indexing, axis 축 이해 및 관련 함수활용하기] (0) | 2020.04.15 |
|---|---|
| (SM) 융합연구 - numpy모듈(3) [연산, 통계, 합계, 조건 함수와 broadcasting이해하기] (0) | 2020.04.15 |
| (SM) 융합연구 - numpy모듈(1) [numpy란?, 데이터 생성하기] (1) | 2020.04.15 |

최근댓글