1번 글에서는 '오차 역전파'를 통해서 역방향 계산을 하는 과정을 포스팅 했었다.
실제로는 경사하강법은 '손실함수'라는 개념을 사용하여 나온 방법이다.
경사하강법의 정의 :
'어떤 손실함수(loss function)가 정의되었을 때, 손실 함수의 값이 최소가 되는 지점을 찾아가는 방법'
앞에서 본 결과는 손실 오차 중 제곱오차(Squared Error)를 미분한 결과와 동일하다.
■ 손실함수란 무엇인가?
어떤 모델이 좋은 모델이고 어떤 모델이 안좋은 모델일까?
그것에 대한 기준은 무엇일까?
모델A가 모델 B보다 좋은 모델이다.' = '모델 A가 모델 B보다 나쁘지 않은 모델이다.'
라는 아이디어에서 착안하여
모델의 적합성을 판단하는 기준 : 오차의 정도
(이 글에서는 손실함수 중 제곱 오차(SE)를 사용한다.)

Q1. 왜 제곱을 할까?
y - y_hat의 값이 양수도 될 수 있고, 음수도 될 수 있다.
y와 y_hat이 얼마나 떨어져 있는지를 오차의 부호에 상관없이 측정하기 위해
Q2. 손실함수 값의 최솟값은 어떻게 찾을까?
앞 글에서와 동일하게 "미분"을 통해서 찾는다.
SE를 w(가중치)에 대해서 미분을 하게 되면,
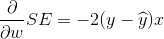
2는 상수이므로 생략을 해주어 -(y-y_hat)*x가 되고,
(오차 역전파에서 w_rate와 동일)
SE를 b(절편)에 대해서 미분한 결과는

(b_rate와 동일)
이렇게 제곱오차에 대해서 미분을 한 이후에
손실함수의 낮은 쪽으로 이동하기 위해서는
각 값에서 변화율을 빼준다.
※ 왜 변화율(미분한 값)을 빼주어야 하는 것일까?
x축은 w
y축은 SE인 두 그래프이다.
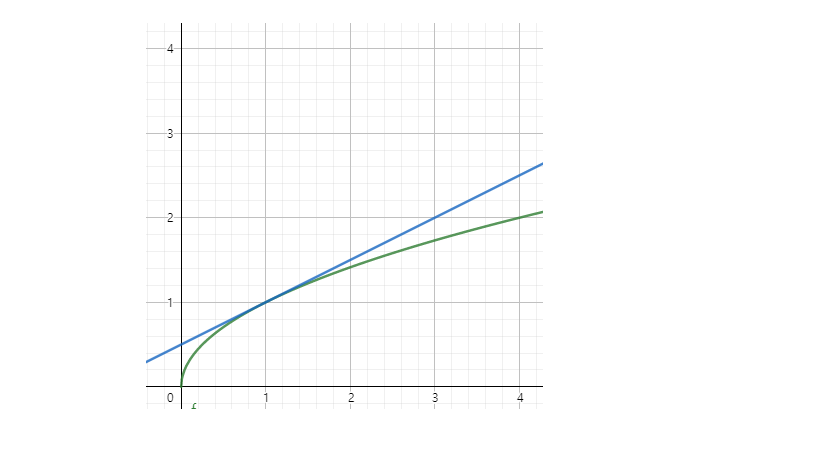
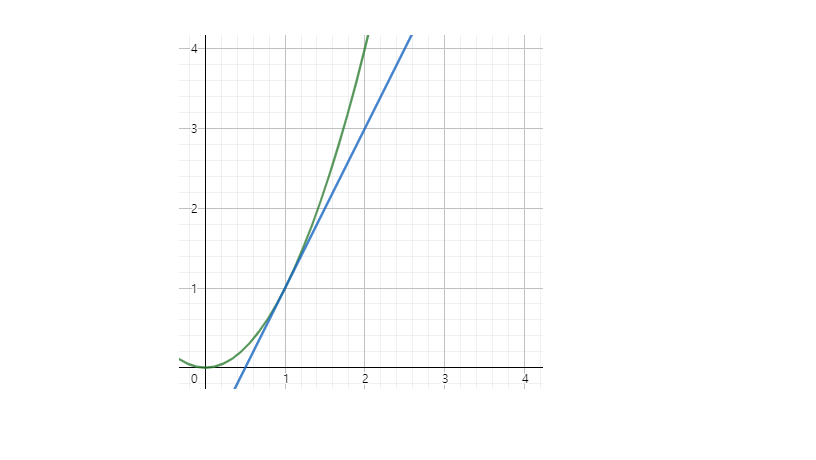
'w - 변화율' 을 해줄때,
1번 그래프는 변화율이 양수이므로 x축(w)의 음의 방향으로 이동을 한다.
2번 그래프는 변화율이 음수이므로 x축(w)의 양의 방향으로 이동을 한다.
'w-변화율'로 인해 SE는 항상 작아지는 방향으로 이동을 하는 것을 볼 수 있다.
(그래프의 함수는 단지 예를 들기 위해 관련이 없는 함수로 적용을 했다.)
W, b 업데이트 :
○ W = W + (y - y_hat) * x
○ b = b + (y - y_hat) * 1
이처럼 인공지능 분야에서 '변화율'은 아주 자주 쓰이는 개념이다.
변화율은 인공지능 분야에서 Gradient (그레이디언트) 라는 용어를 사용한다.
'기계학습 > Machine Learning' 카테고리의 다른 글
| [Hands-on Machine Learning] Machine Learning (의미와 종류) (0) | 2020.07.03 |
|---|---|
| 회귀분석 - 단순 선형 회귀분석 (0) | 2020.03.02 |
| (JH)선형회귀(Linear Regression) - Do it 딥러닝 입문 1 (0) | 2020.02.29 |
| (JH) 텐서플로우 기본 개념과 용어 2 (placeholder) (0) | 2020.02.27 |
| (JH) 텐서플로우 기본 개념과 용어 1 (0) | 2020.02.27 |

최근댓글