1. 회귀분석
1) 회귀분석의 정의
하나 이상의 독립변수들이 종속변수에 미치는 영향을 추정하는 통계 기법
X의 정보를 활용해서 Y를 예측하는 방법
2) 회귀분석의 변수
X(영향을 주는 변수) : 입력변수, 설명변수, 독립변수, 예측변수
Y(영향을 받는 변수) : 출력변수, 반응변수, 종속변수, 결과변수
2. 단순 선형 회귀분석
하나의 독립변수가 종속변수에 미치는 영향을 추정할 수 있는 통계법
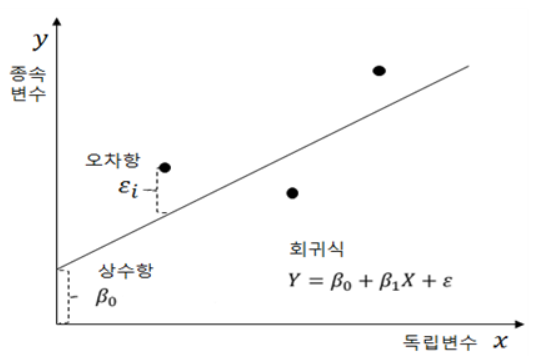
1) 단순 선형 회귀분석의 구성
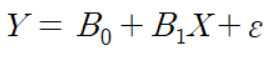
B0 : 절편
B1 : 기울기
ε : 오차항
B0과 B1은 회귀계수로도 불림
2) 최소제곱법(최소자승법)을 이용한 회귀계수의 추정
실제 값의 오차의 제곱의 합이 최소가 되는 값을 구하는 방식으로 잔체제곱이 가장 작은 선을 구하는 것
최소제곱법 : 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법
잔차 : 실제 값과 추정값의 차이
◈잔차제곱합(SSE; Error Sum of Squares) 구하기
- 잔차의 합이 아닌 잔차제곱합을 구하는 이유 : 잔차의 합이 0이 되는 경우는 유일하지 않고, 잔차의 절댓값의 합은 미분이 불가하다. → 잔차제곱합을 이용하면 미분 가능한 형태로 유일한 경우를 찾을 수 있다.
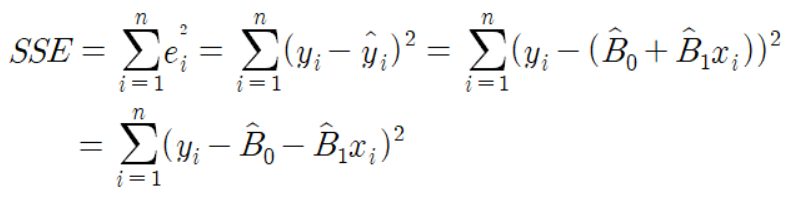
잔차제곱합이 최소가 되도록 하고, B0 과 B1 의 값을 구하기 위해서는 위의 식을 미분한다.
미분한 결과, 아래 두 식을 얻을 수 있다.

이 식을 정리하면, 회귀계수인 절편과 기울기를 추정할 수 있다.
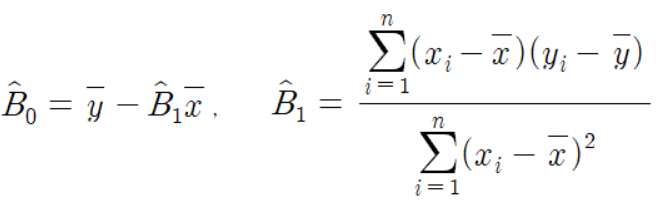
선형회귀에서는 잔차제곱합을 최소화하는 방식으로 회귀계수를 추정하므로 SSE의 값이 작을수록 좋은 모델이라고 해석할 수 있다.
3) 회귀분석의 검정
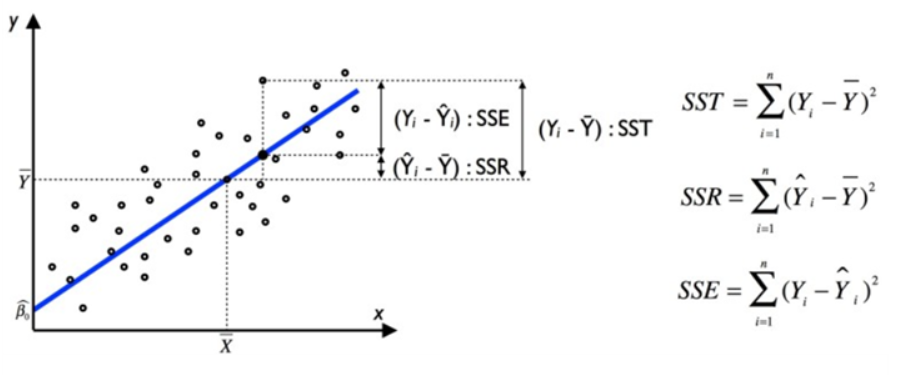
전체제곱합(SST; Total Sum of Squares) : 변인 값과 평균 사이의 편차를 제곱한 값들의 총합(SSR + SSE)
회귀제곱합(SSR; Regression Sum of Squares) : 예측값에서 평균을 뺀 수치를 제곱한 값들의 총합
결정계수 : 전체제곱합에서 회귀제곱합의 비율(SSR / SST)
결정계수가 1에 가까울수록 회귀식이 타당하고 설명력이 있음을 의미한다.
| 요인 | 자유도 | 제곱합 |
| 회귀 | K | SSR |
| 잔차 | n-K-1 | SSE |
| 전체 | n-1 | SST |
<Reference>
'기계학습 > Machine Learning' 카테고리의 다른 글
| [Hands-on Machine Learning] Machine Learning (더 좋은 알고리즘 학습을 위한 선택) (1) | 2020.07.03 |
|---|---|
| [Hands-on Machine Learning] Machine Learning (의미와 종류) (0) | 2020.07.03 |
| (JH) 선형회귀(Linear Regression) - Do it 딥러닝 입문 2 (0) | 2020.03.01 |
| (JH)선형회귀(Linear Regression) - Do it 딥러닝 입문 1 (0) | 2020.02.29 |
| (JH) 텐서플로우 기본 개념과 용어 2 (placeholder) (0) | 2020.02.27 |

최근댓글