회귀
지도학습은 2가지 유형, 분류와 회귀로 나뉜다.
분류 - 예측값이 카테고리와 같은 이산형 값
회귀 - 예측값이 연속형 숫자
회귀는 그 중에서도 선형회귀가 가장 많이 사용된다. 선형 회귀는 직선형 회귀선을 예측값과 실제값의 차이가 가장 작게 산출되도록 가중치들을 최적화하여 찾아내는 방식을 의미한다.
단순 선형 회귀
단순 선형 회귀는 독립변수(X) 하나, 종속변수(Y)도 하나인 선형 회귀를 의미한다. 독립변수와 종속변수가 갑자기 나와서 헷갈릴 수도 있지만, 쉽게 말해 독립변수는 피처를, 종속변수는 레이블 값을 의미한다. 따라서 단순 선형 회귀는 피처가 하나인 데이터를 가장 잘 나타내는 회귀선을 찾는 기법이라고 생각하면 된다.
X, Y를 좌표평면에 찍고, 그 점들을 가장 잘 표현할 수 있는 직선을 찾아내는 것이다. (가장 잘 표현한다는 의미는 예측값과 실제값의 차이가 가장 작은 것을 의미한다.) 최종적으로 알아내야 하는 회귀선의 방정식은

이다. 실제 Y(레이블 값)가 아니라 회귀 식을 통해서 예측을 했다는 의미로 Y_hat을 사용한다.
오차 값을 구하는 방법
데이터를 가장 잘 표현하는 직선을 찾아내기 위해서 오차가 가장 작도록 w_0, w_1을 찾아내야 한다. 그럼 직선과 점들의 오차를 단순히 다 더하면 되는 것일까?
데이터 중에서는 직선의 예측값보다 큰 값도 존재하고, 작은 값도 존재한다. 이로 인해 (실제값 - 예측값) 혹은 (예측값 - 실제값)을 하는 경우에 양의 값과 음의 값이 둘 다 나오게 된다. (통상적으로 오차는 실제값에서 예측값을 뺀 값을 사용한다.) 그런 상황에서 단순히 오차의 합을 더하게 된다면, 다른 부호의 값들이 더해져 오차가 상쇄되는 현상이 일어나 실제 오차를 정확하게 반영하지 못하는 현상이 일어나게 된다. 이런 현상을 방지하기 위해서 크게 2가지 방법으로 오차값을 산출한다.
1. 절댓값을 취해서 더한다. (Mean Absolute Error)
2. 제곱을 구해서 더한다. (RSS, Residual Sum of Square)
이 방법들 중에서도 2번째인 오차를 제곱하는 방식을 더 자주 사용한다. 그 이유는 뒤에서 얘기할 경사하강법과 관련이 있다.
RSS
앞에서 왜 오차의 제곱을 더한 값들이 오차값의 기준이 되는지에 대해서 알아보았다.
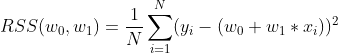
식을 보면, 여러가지 문자들이 많이 나와있다. (w_0, w_1, N, y_i, x_i) 이 때문에 이 식이 어렵고 복잡하게 느껴질 수 있지만, 선형 회귀에서 최종적으로 찾아내야 하는 값이 w_0, w_1을 제외한 모든 값들을 데이터의 입력을 통해 받은 정보라는 사실이다.
y_i = i 번째 인덱스의 레이블 값
x_i = i 번째 인덱스의 피처 값
N = 총 데이터의 수, 즉 데이터 행의 수
RSS식의 계산을 통해 나온 값을 비용이라고 하며, w변수로 구성된 RSS 식을 비용함수 또는 손실함수라고 표현한다.
경사하강법
오차의 기준인 비용함수를 알아보았다. 비용 함수의 최소를 구하는 방법으로는 경사하강법이 있다. 위에서 예를 단순 선형 회귀로 예를 들어서 w_i를 쉽게 구할수도 있을 것이라고 생각할 수도 있다. 하지만, 피처가 여러개, 즉 독립변수 X가 여러개가 된다면, 좌표를 통해서 표현하는 것이 복잡해지고, 최소값을 찾아내기도 매우 어려워진다. 경사하강법은 오차를 통해서 각 회귀 계수(w_i)들을 오차를 줄이는 방향으로 업데이트 하는 것을 의미한다. 이로 인해 오차를 줄이는 방향과 업데이트의 양이 경사하강법에서 중요하게 작용한다.
오차를 줄이는 방향
오차를 줄이는 방향에 관해서는 미분을 통해서 정한다. 비용 함수를 미분하여, 미분 계수가 감소하다가 더이상 감소하지 않는 지점을 찾아가는 방향을 찾는다. 회귀 계수에서 비용함수를 해당 회귀 계수로 편미분한 값을 뺴주면, 회귀 계수가 비용함수가 최소가 되는 방향으로 이동한다.
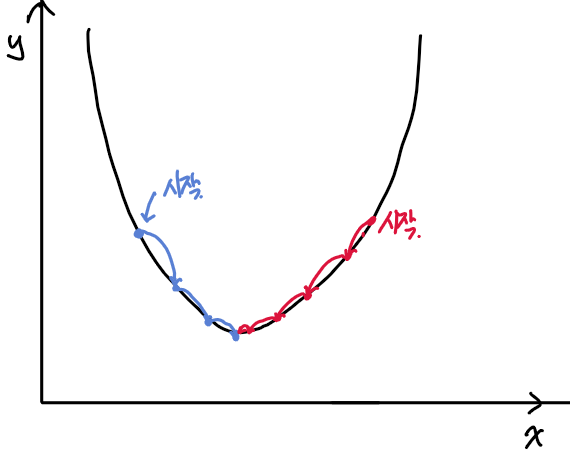
업데이트의 양(학습률)
그렇다면 회귀 계수에서 편미분 한 값 그대로를 빼주면 비용함수의 최소값을 구할수 있는 것일까? 회귀 계수를 업데이트 하는 양에 대해서도 고민을 해봐야 한다. 만약 미분값이 너무 크거나 작다면 회귀 계수를 업데이트 했을 때, 최적 지점을 넘어가게 되거나 아니면 너무 느리게 진행될 것이다. 이것을 위해서 사용자가 하이퍼 파라미터로 직접 지정해주는 학습률이라는 보정 계수를 업데이트 하는 미분 값에 곱해주게 된다.
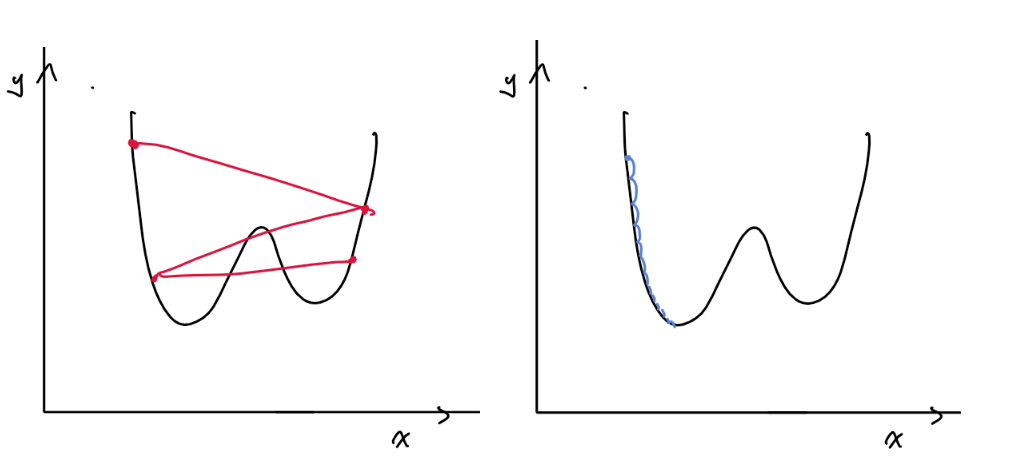
경사하강법의 단점
일반적으로 경사하강법은 모든 학습데이터에 대해서 반복적으로 비용함수를 최소화하기 위한 값을 업데이트 하여 수행시간이 매우 오래 걸린다는 단점을 가지고 있다. 이런 단점을 보완하기 위해서 확률적 경사하강법(Stochastic Gradient Descent)을 사용한다. 일반 경사하강법은 한번 학습하는 과정에서 모든 데이터를 가지고 편미분한 값과 학습값의 곱을 반복하여 업데이트하는 과정이라면, 확률적 경사하강법은 한번 학습할 때 하나의 데이터만 가지고 계수 업데이트를 한다.
한번 학습할 때 모든 데이터를 다루는 것이 아니라 하나의 데이터만 가지고 계산을 수행하여 확률적 경사하강법이 수행시간은 짧다. 일반 경사하강법과 확률적 경사하강법 모두 학습을 반복할수록 최적해에 수렴하는 모습을 보이지만, 일반 경사하강법은 일정하게 최적해에 접근하는 반면, 확률적 경사하강법은 노이즈가 심하다.
대부분은 둘의 절충안인 미니배치 확률적 경사하강법을 사용한다. 사용자가 직접 미니 배치의 개수를 정하고, 한번 학습할 떄 지정한 수만큼의 데이터를 사용하여 가중치를 업데이트 한다.
'기계학습 > Machine Learning' 카테고리의 다른 글
| [파이썬 머신러닝 완벽가이드] - 규제선형 모델 : 릿지, 라쏘 엘라스틱넷 (0) | 2020.09.15 |
|---|---|
| [파이썬 머신러닝 완벽 가이드] : 다항 회귀 ( Polynomial, 편향, 분산) (0) | 2020.09.02 |
| [파이썬 머신러닝 완벽가이드] : 사이킷 런 앙상블 러닝 ( Stacking ) (0) | 2020.08.25 |
| [파이썬 머신러닝 완벽 가이드] : 사이킷런 앙상블 러닝 ( XGBoost / LightGBM) (1) | 2020.08.21 |
| [파이썬 머신러닝 완벽가이드] : 사이킷 런 앙상블 러닝 ( Boosting ) (0) | 2020.08.21 |

최근댓글