회귀
이전 포스팅에서 설명한 회귀의 형태는 y = w_0 * x_0 + .... + w_n * x_n 이었다.
이것은 점들의 관계를 직선으로 표현하는 식이다. 하지만, 모든 현상을 직선으로 표현하는 것이 최선은 아니다. 어느 경우에는 조금 더 복잡하게 하는 경우에 최적의 회귀선을 나타내는 것일수도 있다. 이런 것을 표현하기 위해 다항회귀를 사용한다.
여기에서 "독립변수"가 단항식(x_0 ... x_n)이 아닌 2차, 3차로 표현되는 것을 다항(Polynomial) 회귀라고 한다.
다항이라는 것은 x_0, x_1, x_0 * x_1, (x_0)^2, (x_1)^2 .... 이라고 생각하면 된다.
"독립변수"라는 것을 강조한 이유는 다항회귀면 비선형회귀여야 하는 것이라는 것에 대한 오해를 풀기 위해서이다.
선형회귀와 비선형회귀를 구분하는 것은 "독립변수"의 선형성이 아니라, "회귀 계수"의 선형성이다.
회귀 계수는 선형 회귀를 구현할 때와 마찬가지로 w_0, .... w_n이기 때문에, 다항 선형 회귀이다.
사이킷 런에서는 직접적으로 다항회귀를 구현해주는 클래스를 가지고 있지 않다. 대신, PolynomialFeatures라는
피처를 다항식 피처로 변환해주는 클래스를 이용하여 구현한다.
1. 피처를 PolynomialFeature 클래스를 이용하여 차수를 정하고 다항식 피처로 변환한다.
2. 이후에 선형회귀 클래스인 LinearRegression()을 이용해서 학습 - 예측을 수행한다.
편향 - 분산 트레이드 오프
직선으로 데이터를 표현하는 경우에, 데이터를 충분히 표현하지 못하는 경우가 있다. 이런 경우, 편향이 매우 크다고 이야기한다. 지나치게 특정 방향으로 치우쳐져 있다는 의미이다.
반대로 다항 회귀에서 차수가 너무 큰 경우에는 변동성이 커지고, 이를 고분산성을 가진다고 이야기한다.
위에서 언급한 편향 (Bias)와 분산(Variance)은 한쪽의 성능을 좋게 하면, 나머지 하나의 성능이 떨어지는 트레이트-오프관계에 있다. 쉽게 말해 편향을 줄이면 분산이 늘어나고, 분산을 줄이면 편향이 늘어난다고 보면된다.
따라서 둘의 성능을 적절하게 맞춰 전체 오류가 가장 낮아지는 지점을 '골디락스' 지점이라고 한다. 이 지점을 찾는 것이 매우 중요하다. (단순히 선형회귀 뿐만이 아니라 대부분의 머신러닝 모델이 그렇다!)
실습
단항값 [x_1, x_2]을 2차 다항값으로 [1, x_1, x_2, (x_1)^2, x_1 * x_2, (x_2)^2]로 변환해보자.
from sklearn.preprocessing import PolynomialFeatures
import numpy as np
from sklearn.linear_model import LinearRegression
#다항식으로 변환한 단항식 생성, [[0,1], [2,3]]의 2X2 행렬 생성
X = np.arange(4).reshape(2,2)
print('일차 단항식 계수 피처:\n', X)
#degree = 2인 2차 다항식으로 변환하기 위해 PolynomialFeatures를 이용해 반환
poly= PolynomialFeatures(degree = 2)
poly.fit(X)
poly_ftr = poly.transform(X)
print('변환된 2차 다항식 계수 피처 : \n', poly_ftr)
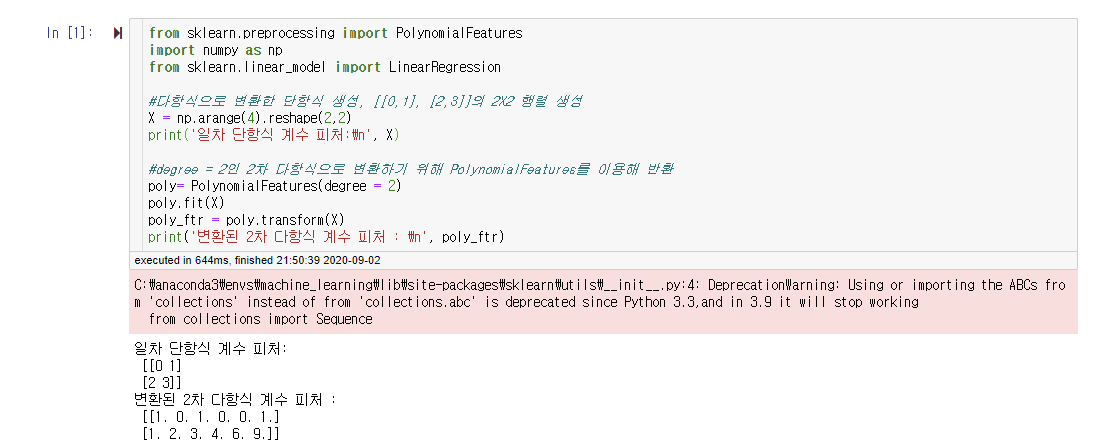
이렇게 단항 피처를 다항식 피처로 변환하고 선형회귀 모델을 이용하여 학습하면 되는 것이다 .
단순히 이런 형태가 아닌 임의로 원하는 다항식을 만드는 경우에는 별도의 함수를 정의해주어야 한다.
여기에서는 y = 1 + 2 * x_1 + 3 * (x_1)^2 + 4 * (x_2)^2로 피처를 다항 피처로 변환한다.
def polynomial_func(X):
y = 1 + 2 *X[:,0] + 3 *X[:,0]**2 + 4 *X[:,1] ** 3
return y
X = np.arange(4).reshape(2, 2)
print('일차 단항식 계수 features : \n', X)
y = polynomial_func(X)
print('삼차 다항식 결정값 : \n', y)
가장 아래 삼차 다항식 결정값을 보면 원하는 값으로 나온 것을 볼 수 있다.
단항 피처를 가지고 3차 다항 피처로 변환한 후에, 선형회귀를 이용하여 회귀계수를 찾아보자.
#3차 다항식 변환
poly_ftr = PolynomialFeatures(degree=3).fit_transform(X)
print('3차 다항식 계수 feature : \n', poly_ftr)
#Linear Regression에 3차 다항식 계수 feature와 3차 다항식 결정값으로 학습 후 회귀 계수 확인
model = LinearRegression()
model.fit(poly_ftr, y)
print('Polynomial 회귀 계수 : \n', np.round(model.coef_, 2))
print('Polynomial 회귀 Shape : \n', model.coef_.shape)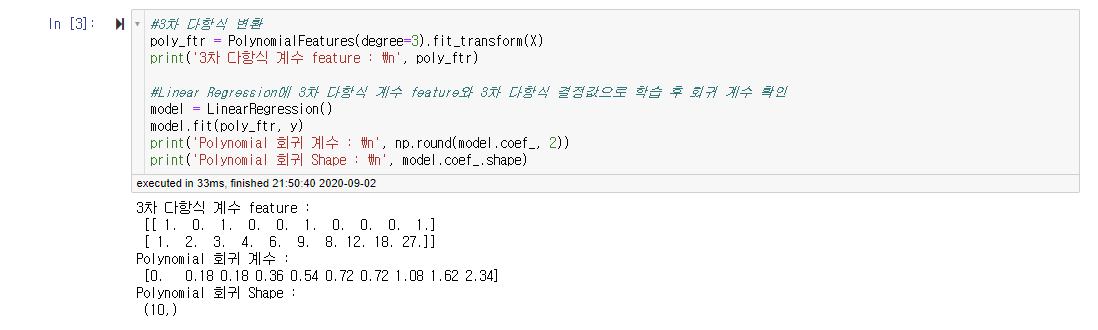
코드의 명료함을 위해서는 피처 변환과 선형회귀의 적용을 한꺼번에 할 수 있도록 Pipeline 클래스를 이용하면 된다.
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import Pipeline
import numpy as np
def polynomial_func(X):
y = 1 + 2*X[:, 0] + 3* X[:, 0]**2 + 4*X[:, 1]**3
return y
#Pipeline 객체로 Streamline 하게 Polynomial Feature 변환과 Linear Regression을 연결
model = Pipeline([('poly', PolynomialFeatures(degree=3)),
('linear', LinearRegression())])
X=np.arange(4).reshape(2,2)
y = polynomial_func(X)
model = model.fit(X, y)
print('Polynomial 회귀 계수 \n', np.round(model.named_steps['linear'].coef_, 2))
그렇다면 직선보다는 훨씬 복잡한 회귀선을 제작하면 성능이 올라가는 것일까?
그렇지 않다! 이전에도 얘기했던 과적합 문제가 발생하게 된다. 너무 주어진 데이터에 편향된 나머지, 오히려 실제 예측값은 성능이 저하되는 현상이 발생하게 된다. 그래서 다항식의 차수를 결정하는 것도 굉장히 중요한데, 이것에 대한 예제로 https://scikit-learn.org/stable/auto_examples/model_selection/plot_underfitting_overfitting.html#sphx-glr-auto-examples-model-selection-plot-underfitting-overfitting-py
Underfitting vs. Overfitting — scikit-learn 0.23.2 documentation
Note Click here to download the full example code or to run this example in your browser via Binder Underfitting vs. Overfitting This example demonstrates the problems of underfitting and overfitting and how we can use linear regression with polynomial fea
scikit-learn.org
가 있다. 내용은 원본 데이터 세트는 피처 X와 y가 잡음(Noise)가 포함된 다항식의 코사인 그래프 관계를 가지도록 만들어주고, 다항피처의 차수를 변화시키면서 예측 정확도를 비교하는 내용이다.
일단 데이터를 설정해준다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import cross_val_score
%matplotlib inline
#임의의 값으로 구성된 X값에 대해 코사인 변환 값을 반환 .
def true_fun(X):
return np.cos(1.5 * np.pi * X)
#X는 0부터 1까지 30개의 임의의 값을 순서대로 샘플링한 데이터
np.random.seed(0)
n_samples = 30
X = np.sort(np.random.rand(n_samples))
#y값은 코사인 기반의 true_fun()에서 약간의 노이즈 변동 값을 더한 값입니다.
y = true_fun(X) + np.random.randn(n_samples) * 0.1
이후에 다항 피처의 차수를 1, 4, 15로 바꾸면서 예측 결과를 비교한다. 이때 cross_val_score()로 교차 검증을 수행하며, 예측 성능 평가는 평균제곱오차(Mean Squared Error)를 사용한다.
plt.figure(figsize = (14,5))
degrees = [1,4,15]
#다항 회귀의 차수(degree)를 1,4,15로 각각 변화시키면서 비교
for i in range(len(degrees)):
ax = plt.subplot(1, len(degrees), i + 1)
plt.setp(ax, xticks=(), yticks=())
#개별 degree 별로 Polynomial 변환합니다.
polynomial_features = PolynomialFeatures(degree = degrees[i], include_bias = False)
linear_regression = LinearRegression()
pipeline = Pipeline([("polynomial_features", polynomial_features),
("linear_regression", linear_regression)])
pipeline.fit(X.reshape(-1, 1), y)
#교차 검증으로 다항 회귀를 평가합니다.
scores = cross_val_score(pipeline, X.reshape(-1, 1), y, scoring = "neg_mean_squared_error", cv = 10)
#Pipeline을 구성하는 세부 객체를 접근하는 named_steps['객체명']을 이용해 회귀 계수 추출
coefficients = pipeline.named_steps['linear_regression'].coef_
print('\nDegree {0} 회귀 계수는 {1} 입니다. '.format(degrees[i], np.round(coefficients, 2)))
print('Degree {0} MSE는 {1} 입니다.'.format(degrees[i], -1*np.mean(scores)))
#0부터 1까지 테스트 데이터 세트를 100개로 나눠 예측을 수행합니다.
#테스트 데이터 세트에 회귀 예측을 수행하고 예측 곡선과 실제 곡선을 그려서 비교합니다.
X_test = np.linspace(0, 1, 100)
#예측값 곡선
plt.plot(X_test, pipeline.predict(X_test[:, np.newaxis]), label="Model")
#실제 값 곡선
plt.plot(X_test, true_fun(X_test), '--', label="True function")
plt.scatter(X, y, edgecolor='b', s=20, label="Samples")
plt.xlabel("x"); plt.ylabel("y"); plt.xlim((0,1));plt.ylim((-2,2)); plt.legend(loc="best")
plt.title("Degree {}\nMSE = {:.2e}(+/- {:.2e})".format(degrees[i], -scores.mean(), scores.std()))
plt.show()
결과를 확인하면, 다항식의 차수가 지나치게 높아지면 오히려 더 왜곡되는 것을 확인할 수 있다. 반면에 차수가 너무 작으면 데이터를 충분히 표현하지 못한다. 그래서 최적의 차수를 정하는 것이 다항회귀에서 매우 중요하다.
'기계학습 > Machine Learning' 카테고리의 다른 글
| [파이썬 머신러닝 완벽 가이드] 전처리, 로지스틱 회귀, 회귀 트리 (0) | 2021.07.08 |
|---|---|
| [파이썬 머신러닝 완벽가이드] - 규제선형 모델 : 릿지, 라쏘 엘라스틱넷 (0) | 2020.09.15 |
| [파이썬 머신러닝 완벽 가이드] : 회귀 ( 선형 회귀 / 경사하강법) (0) | 2020.08.30 |
| [파이썬 머신러닝 완벽가이드] : 사이킷 런 앙상블 러닝 ( Stacking ) (0) | 2020.08.25 |
| [파이썬 머신러닝 완벽 가이드] : 사이킷런 앙상블 러닝 ( XGBoost / LightGBM) (1) | 2020.08.21 |

최근댓글