(JY) Keras 사용해보기
1. What is keras? 케라스(Keras)는 텐서플로우 라이버러리 중 하나로, 딥러닝 모델 설계와 훈련을 위한 고수준 API이다. 사용자 친화적이고 모델의 구성이 쉽기 때문에 기본 이미지 분류 및 텍스트 분��
dsbook.tistory.com
위 함수의 모델을 구성하고 훈련하는 과정에서 fully-connected layers, 완전연결 계층으로 모델을 구성하고 학습시켜 분류한다고 했었다. 그럼 여기서 완전연결 계층이 무엇이고, 어떤 역할을 하는지 차근차근 알아보자.
model = keras.Sequential()
model.add(layers.Flatten(input_shape = (28, 28))) # 1
model.add(layers.Dense(128, activation='relu')) # 2
model.add(layers.Dense(10, activation='softmax')) # 3
1. 완전연결 계층, Fully connected layer
"완전 연결 되었다"는 뜻은 한 층(layer)의 모든 뉴런이 그 다음 층(layer)의 모든 뉴런과 연결된 상태를 말한다. 1차원 배열의 형태로 평탄화된 행렬을 통해 이미지를 분류하는데 사용되는 계층이다. Fully connected layer을 Dense layer이라고도 한다. 위의 코드에서는 Flatten을 통해 흑백 이미지, 2차원 벡터의 행렬을 1차원 배열로 평탄화 하고, Relu함수로 뉴런을 활성화하고 softmax함수로 이미지를 분류하는 것까지가 Fully connected layer라고 할 수 있다.
여기서 한 가지 중요한 것은 우리가 fashion mnist에서 사용한 이미지는 "흑백"이미지 라는 것이다. 흑백이미지는 흑과 백의 명암으로만 이미지가 구성되기 때문에 RGB를 사용하는 컬러이미지와는 달리 벡터를 1차원 행렬로 변환시키는데 아무런 어려움이 없다. 앞서 본 train_images가 3차원 넘파이배열로 나타난 것도 바로 그 이유이다. (60000, 28, 28)에서 60000은 이미지의 갯수를 뜻하고, 그 뒤의 28, 28는 각각 가로와 세로의 크기를 나타낸 것이다. 만약 이 이미지가 RGB 필터의 픽셀값을 가진 컬러이미지였다면 (60000, 3, 28, 28)의 4차원 넘파이 배열로 나타났을 것이다. 여기서 3은 RGB의 채널의 갯수를 말한다. 이럴 경우, 단순히 3차원 이미지를 1차원으로 평탄화하면 공간 정보가 손실될 수밖에 없으며, 이럴 경우 정보 부족으로 인해 이미지를 분류하는데 한계가 생길 수밖에 없다.
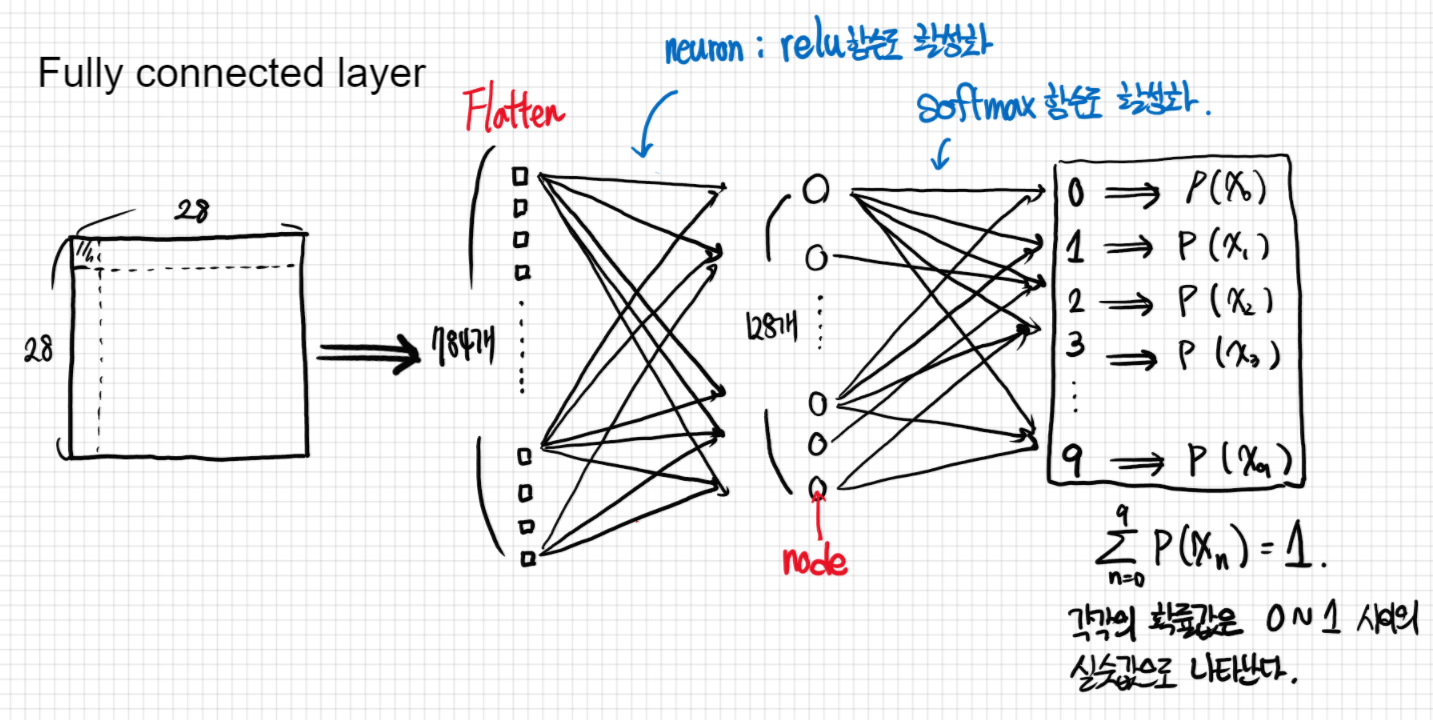
2. 활성화 함수, Activation function
각 노드마다 값이 존재하고 뉴런마다 가중치와 편향(bias)값이 존재하여 다른 계층으로 넘어갈 때, 각 노드에 가중치를 곱하고 편향을 더한 값이 넘어가게 된다. 이때 활성화 함수가 개입되는데, 그 값이 특정 조건을 만족하게 되면 활성화되었다는 신호를(활성화 함수를 거친 출력값) 다음 노드로 보내 활성화하고, 만약 조건을 만족하지 못했으면 해당 노드를 비활성화하는 함수가 활성화 함수이다. (신경학적으로 볼 때 뉴런 발사 과정에 해당한다.)
다양한 활성화 함수가 있으며, 어떤 활성화 함수를 사용하는지에 따라 그 출력값이 달라지기 때문에 어떤 문제를 해결하느냐에 따라 적절한 활성화 함수를 사용하는 것이 중요하다. 우리는 앞서 사용했던 ReLU함수와 Softmax 활성화 함수에 대해 알아보자.
1) ReLU 함수 ( Rectified Linear Unit )
$$f(x) = \begin{cases}0 & x<0\\x & x \geq 0\end{cases}$$
세상 간단하면서도 많이 사용되는 활성화 함수 중 하나이다. 위의 그래프에서 푸른색 그래프가 ReLU함수이다. 수식만 봐도 알 수 있듯이 입력값이 음수면 0으로 비활성화 하고, 입력값이 양수면 해당 값을 그대로 출력하는 활성화 함수이다. 주로 딥러닝에서 연구하는 컴퓨터 비전 분야와 음성인식 분야에 자주 사용된다. 이 함수가 자주사용되는 이유는 바로 다음에 있다.
- 경사 전파 (Gradient propagation) : 위 함수의 기울기 그래프는 x가 음수면 0, 양수면 1로 나타나는 unit-step function과 동일하다. 따라서 sigmond 활성화 함수에 비해 소실되는 기울기가 적어 학습에 용이하다. 이후 오차역전파(back propagation)에 대해서 공부하면 이 내용에 대해 더 잘 이해할 수 있을 것이다.
- ReLU함수의 비선형성을 이용해서 사전훈련 없이도 신경망 훈련을 가능하게 하며, sigmond 함수나 다른 비슷한 활성화 함수와 비교했을 때, 더 많고 복잡한 데이터 셋에서 더 빠르고 효과적인 훈련을 가능하게 한다.
2) Softmax 함수
$${softmax(x_i)} = \frac{\exp(x_i)}{\sum_{j=1}^n\exp(x_j)}$$
소프트맥스(softmax)함수는 로지스틱 회귀의 일반화 버전인 소프트맥스 회귀에 사용되는 함수이다. 여기서 로지스틱 회귀란, 0과 1을 구분하는 2진 분류 문제에 사용되는 분류법인데, 소프트맥스 회귀의 경우 이를 일반화하여 다중 분류 문제 해결에 적용할 수 있는 분류법이고, 이 문제를 해결하기 위해 제시된 아이디어가 바로 소프트맥스 함수인 것이다.
소프트맥스의 함수에 실수값을 가진 K개의 벡터를 입력하면, 각각의 요소들 정규화 하여 0~1사이의 값으로 출력된다. 이때 이 K개의 확률값의 합은 1이 되어야 한다. 아래 사진처럼 소프트맥스 함수가 3개의 요소를 입력받으면 각각의 요소가 정규화되어 y1, y2, y3로 출력된다. 여기서 중요한 것은, exp를 통해 정규화 한다는 것이다. 지수함수의 그래프는 x값이 증가함에 따라 기하급수적으로 커진다. 따라서 단순하게 정규화를 진행하는 것이 아니라 최댓값을 보다 극대로 확장시켜 다른 요소들과의 차이를 증폭시킬 수 있다는 것이다.

3. Summary
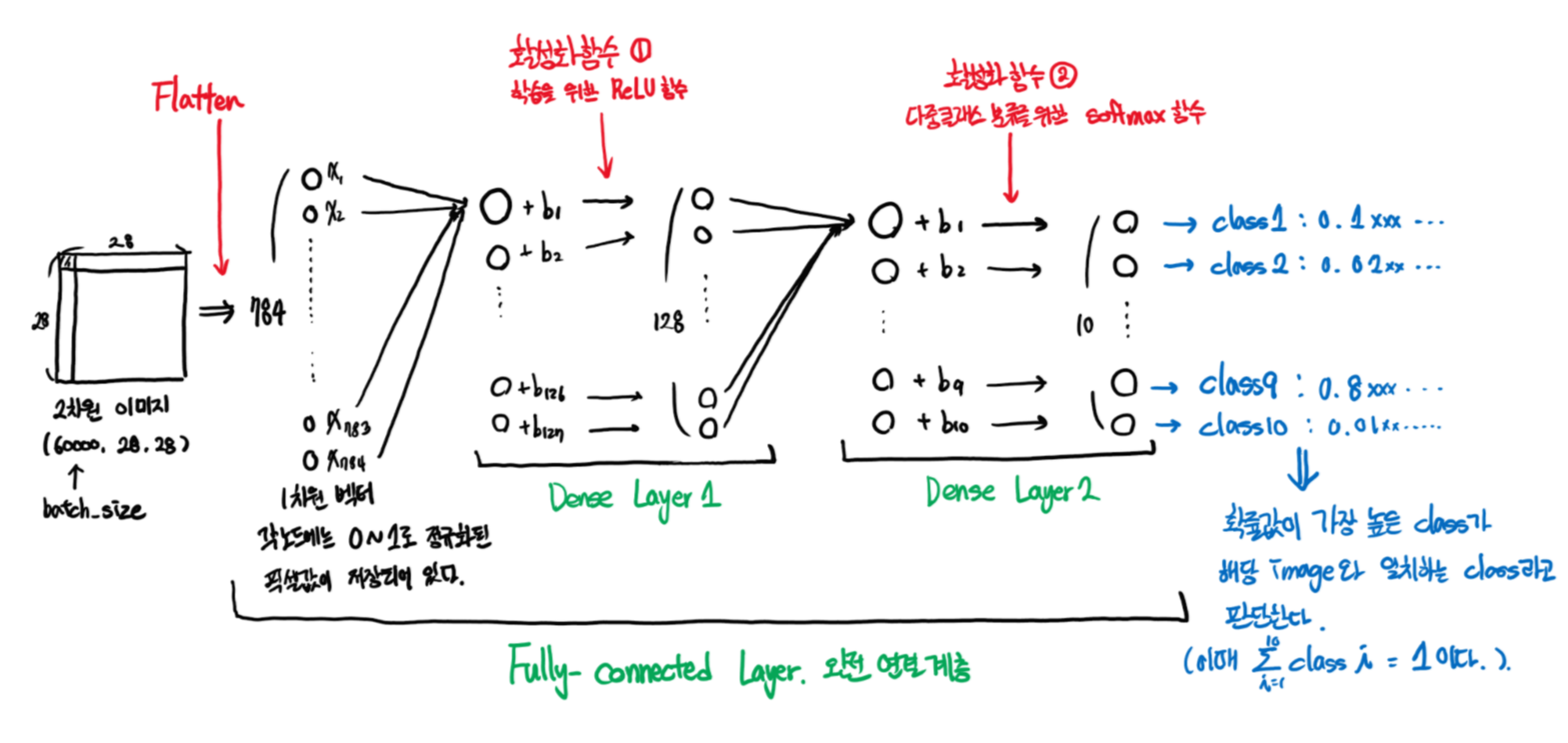
'데이터 사이언스 메뉴얼 > Object classification' 카테고리의 다른 글
| 합성곱 신경망, Convolutional Neural Network (CNN) (1) | 2020.05.28 |
|---|---|
| 최적화, Optimizer (0) | 2020.05.23 |
| 손실 함수, Loss function (0) | 2020.05.17 |
| Keras 사용해보기 (2) | 2020.05.11 |
| 텐서플로우, Tensorflow (0) | 2020.05.07 |



최근댓글