이전까지의 실습 내용을 통해서 데이터를 전처리하였고, 이번 실습에서는 전처리된 데이터가 어떤 그래프 형태를 지니는지, 어떤 특성을 가지고 있는지를 시각화하는 실습을 진행할 것이다. 그 후 각 Column 들 간의 상관도를 계산할 것이다.
시각화
raw_fe.describe(include = 'all').T보통 df.describe() 혹은 df.describe().T를 통해서 데이터의 기본적인 통계적 특성을 확인한다. 여기에서 include = 'all'이라는 옵션을 설정해주게 되면, 수치로 된 데이터가 아닌, object 형태의 데이터나, category 형태의 데이터 또한, 생략하지 않고 보여준다.

히스토그램
raw_fe.hist(bins = 20, grid = True, figsize = (16,12))
plt.show()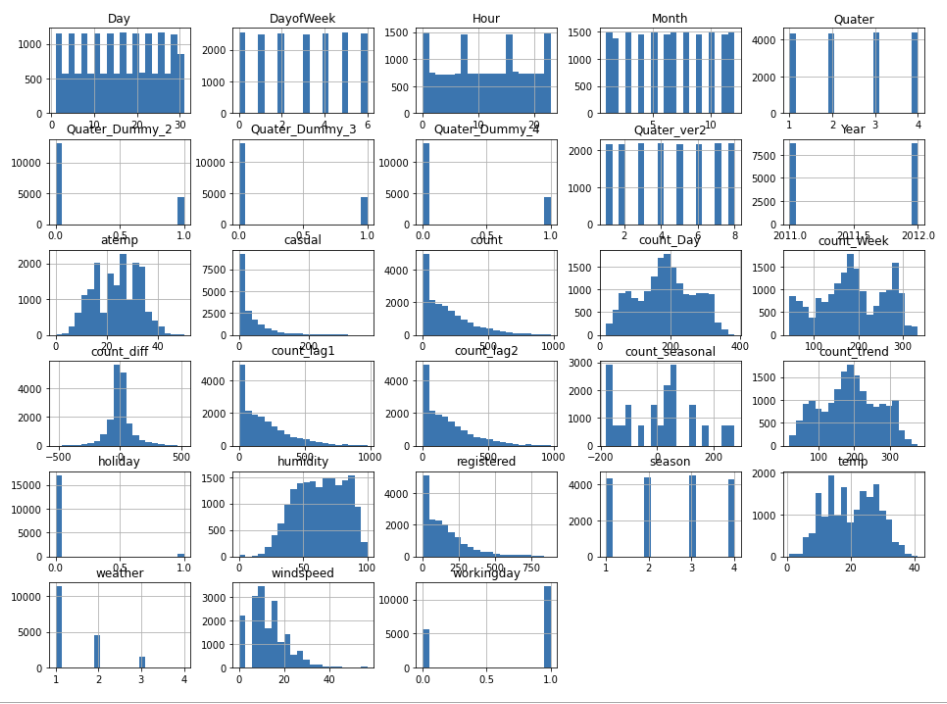
히스토그램이라는 표현이 어색하다면, 간단하게 막대그래프라고 이해하면 된다. 특정 Series의 형태가 아닌 DataFrame 자체를 df.hist( ) 로 시각화 하면, DataFrame 내에 있는 모든 column들에 대한 히스토그램이 그려지게 된다.
인자로 넣은 bins는 x축의 단위의 개수(최대로 나올 수 있는 막대의 개수)이다.
박스 플롯(Box Plot)
raw_fe.boxplot(column='count', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='registered', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='casual', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)

Box Plot에 관해서 간단하게 설명을 하자면, 실선으로 되어있는 네모 영역이 25% ~ 75%의 데이터가 존재하는 구간이고, 초록색 가로선이 중앙값(Median)을 나타낸다. 박스 바깥에 있는 짧은 검은 색 가로선은 Outlier를 제외한 최댓값 혹은 최솟값을 의미한다. 그 범위 밖의 검은 색 점들은 Outlier를 의미한다.
count, registered, casual에 각각 있는 4개의 Box Plot(봄, 여름, 가을, 겨울)의 모형이 유사하다면, 이 값들은 계절(Season)과 관계가 없다는 것을 알아낼 수 있다.
평일, 주말에 따른 자전거 수요 변화 Box Plot
raw_fe.boxplot(column='count', by='holiday', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='count', by='workingday', grid=True, figsize=(12,5))
plt.ylim(0,1000)
평일, 주말을 시간 단위로 자전거 수요 Box Plot
raw_fe[raw_fe.holiday == 0].boxplot(column = 'count', by = 'Hour', grid = True, figsize = (12, 5))
plt.show()
raw_fe[raw_fe.holiday == 1].boxplot(column = 'count', by = 'Hour', grid = True, figsize = (12, 5))
plt.show()

이전에 실습에서 진행한 전처리로 인해서, 코드를 조금만 바꾸게 되더라도, 내가 원하는 정도의 세부적인 정보를 시각화하는 것이 용이하다.
산점도 (Scatter Plot)
방금 위에서 Box Plot으로 시각화 한 내용을 그대로 산점도로 시각화를 하게 되면
raw_fe[raw_fe.holiday == 0].boxplot(column = 'count', by = 'Hour', grid = True, figsize = (12, 5))
plt.show()
raw_fe[raw_fe.holiday == 1].boxplot(column = 'count', by = 'Hour', grid = True, figsize = (12, 5))
plt.show()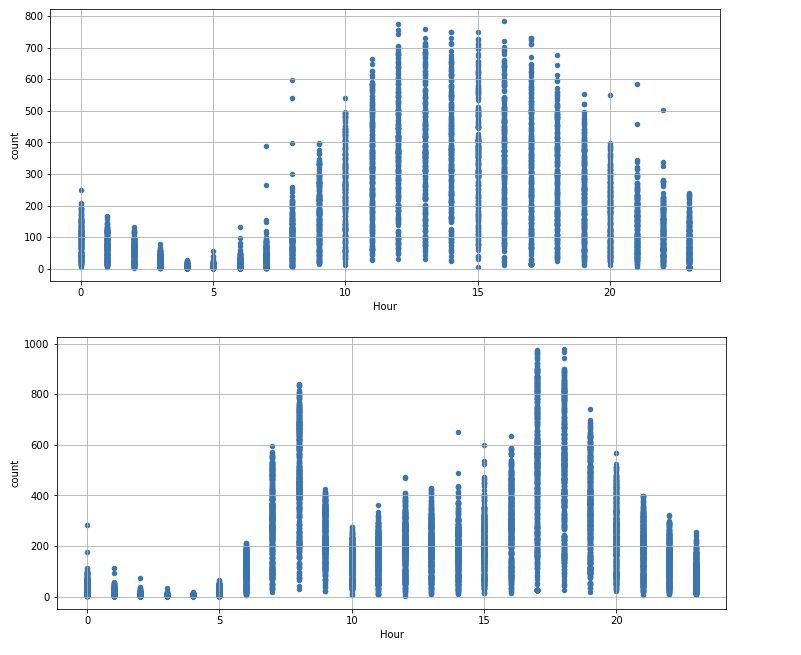
바로 위의 Box Plot과 동일한 형태인 것을 확인할 수 있다.
단순히 여기에서 끝내는 것이 아니라, 산점도라는 2차원 평면에서 온도(temp)를 하나 더 추가해보자.
raw_fe[raw_fe.workingday == 0].plot.scatter(y='count', x='Hour', c='temp', grid=True, figsize=(12,5), colormap='viridis')
plt.show()
raw_fe[raw_fe.workingday == 1].plot.scatter(y='count', x='Hour', c='temp', grid=True, figsize=(12,5), colormap='viridis')
plt.show()
온도가 추가되어, 각 점들마다 색깔이 다르게 표현이 되어있는 것을 확인해 줄 수 있다. 2차원 평면임에도 불구하고, 코드에서 c = 'temp'를 추가함으로써, 한가지 정보를 더 시각화하는 것이 가능하다.
상관도
"상관 분석 또는 '상관관계' 또는 '상관'은 확률론과 통계학에서 두 변수간에 어떤 선형적 또는 비선형적 관계를 갖고 있는지를 분석하는 방법이다. 두 변수는 서로 독립적인 관계이거나 상관된 관계일 수 있으며 이때 두 변수간의 관계의 강도를 상관관계라 한다."
(위키 백과)
상관도는 -1 에서 1까지의 값을 가지며, 1에 가까울수록 두 데이터가 정비례함을, -1에 가까울수록 두 데이터가 반비례함을 나타낸다. 이것을 DataFrame의 각 Column들의 correlation을 한꺼번에 계산을 할 수가 있다.
하지만, 워낙 Column이 많고, 우리가 원하는 데이터는 대부분 1에 가깝거나, 0에 가깝거나, -1에 가까운 값들이다. 따라서, 해당 상관도에 따라서 색을 다르게 표현하는 방법을 사용한다.
raw_fe.corr().style.background_gradient()
코드 한줄로 이렇게 많은 Column들의 상관도를 바로 계산할 수 있고, 이 값들이 너무 상세하다면 소숫점 둘째자리까지만 보여줄수도 있다.
raw_fe.corr().style.background_gradient().set_precision(2)
Reference :
패스트 캠퍼스 파이썬을 활용한 시계열 분석 A-Z
'딥러닝 > 시계열' 카테고리의 다른 글
| 현실적인 데이터 전처리 (0) | 2021.03.05 |
|---|---|
| 시계열 분석 실습 코드 - 6 ( OLS, 검증 지표) (0) | 2021.03.04 |
| 시계열 분석 실습 코드 - 4 (0) | 2021.02.19 |
| 시계열 분석 실습 코드 - 3 (0) | 2021.02.18 |
| 시계열 데이터 분석 코드 - 2 (0) | 2021.02.17 |

최근댓글