저번 실습을 진행한 결과, 간단한 모델을 사용해서 예측을 진행했음에도, R-squared의 값이 1.0이 나왔다.
이것을 조금 더 현실적인 부분을 반영해서 데이터 전처리를 진행해보자.
왜 R-squared 값이 1이 나왔을까?
Test Data의 정보를 Train Data에 반영했기 때문이다.
그렇다면 Test Data는 알려지지 않은 데이터를 어떻게 가정하고 풀어야 하는가?
1. Training Data의 특성이 그대로 반복된다고 가정한다.
2. 한단위씩 예측을 수행하고, Training Data를 갱신해나가면서 학습 및 예측을 수행한다.
특히, 2번에 관해서는 1스텝 교차 검사, 2스텝 교차검사 등이 있다. 기존에 시계열 분석에서 Train Data와 Test Data를 분리하는 경우에는 특정 시점을 기준으로, 해당 시점 이전은 Train Data, 해당 시점 이후는 Test Data로 선정하였다.

1스텝 교차검사와 2스텝 교차검사를 보면, 한꺼번에 모든 Test 기간을 예측하는 것이 아니라, 한 단위씩 예측하고, 그 다음 단계에서는 예측한 값을 다시 Train Data에 포함하여 학습을 한 뒤 그 다음 단위를 예측하는 방식으로 진행한다.
Trend 데이터 전처리
이전에는 Trend에 대한 데이터를 전체 DataFrame에 추가한 뒤에 Train Data와 Test Data를 분리하여, Test Data에도 Trend 데이터가 들어가게 되었다. 하지만, Test데이터의 Y값을 모른다고 가정을 했는데, Trend 값이 데이터에 있는 것은 상식적으로 불가능하다.
Test Data에 Trend를 추가하기 위해서는 Train Data에 포함되어 있는 Trend 데이터를 Test Data에 그대로 반복해야한다.
일단 Trend Data를 시각화해보자.
raw_fe['count_trend'].plot()
plt.show()
Train Data는 2011년 상반기, 하반기, 2012년 상반기까지를 포함하고, Test Data는 2012년 하반기를 포함한다.
하지만, 2011년 하반기의 Trend를 2012년 하반기 Trend에 대입하게된다면, Trend가 부자연스럽게 꺾여버리게 된다.
따라서, 2011년의 Trend를 2012년 Trend에 대입하는 방법을 선택하였다.
raw_fe.loc['2012-01-01' : '2012-12-31','count_trend'] = raw_fe.loc['2011-01-01','count_trend'].values
하지만, 이렇게 대입을 하려고 코드를 입력하면 에러가 발생하는 것을 볼 수 있다.
그 이유는, 2011년에는 2월 29일이 존재하지 않지만, 2012년에는 2월 29일이 존재하기 때문이다.
이 문제의 해결책 그 자체에 주목하기 보다는,
현실적인 데이터 분석에서는 이렇게 우리가 전혀 고려하지 못한 부분에서도 우연히 에러가 발생할 수 있다는 것을 항상 생각하고 있어야 한다.
2011년 2월 28일의 마지막 데이터와, 2011년 3월 1일의 첫번째 데이터를 25등분 하여, 2월 29일의 데이터에 순차적으로 대입한다.
(이 방법이 무조건적인 것은 아니다. 상황에 따라서 임의로 지정할 수 있다.)
#일단 2월 29일을 제외한 나머지 날들의 데이터를 대입한다.
raw_fe.loc['2012-01-01' : '2012-02-28', 'count_trend'] = raw_fe.loc['2011-01-01' : '2011-02-28', 'count_trend'].values
raw_fe.loc['2012-03-01' : '2012-12-31', 'count_trend'] = raw_fe.loc['2011-03-01' : '2011-12-31', 'count_trend'].values
step = (raw_fe.loc['2011-03-01 00:00:00', 'count_trend'] - raw_fe.loc['2011-02-28 23:00:00', 'count_trend'])/25
step_value = np.arange(raw_fe.loc['2011-02-28 23:00:00', 'count_trend'] + step,
raw_fe.loc['2011-03-01 00:00:00', 'count_trend'], step)
step_value = step_value[:24]
raw_fe.loc['2012-02-29','count_trend'] = step_value
이 코드에서는 나머지 날짜들은 기존의 방식대로 2011년의 데이터를 2012년에 대입하고, 2월 29일의 데이터를 설명한 방식으로 채워넣은 것을 확인할 수 있다.
Count_lag1,2
count_lag1,2는 기존의 Y데이터를 한칸(1), 혹은 두칸(2)씩 뒤로 미뤄서 데이터의 시간적인 특성을 고려해 설명 변수 X의 값들이 추후에 Y에 영향을 미치는 것에 대해서 확인할 수 있는 장치이자 특성이었다.
하지만, 이전에는 먼저 count_lag1,2 column을 생성하고, Train_test_split을 진행하였기 때문에, Train Data와 Test Data의 정보가 서로 이어지게 되었다. Test Data 가장 첫번째 데이터는 NaN 값이 되어야 하며, 이것은 .fillna(method = 'bfill') 을 통해서 채워져야 한다.
이렇게 구현하기 위해서는 먼저 Train Data와 Test Data를 분리하고 각각에 대해서 .shift( ) 를 통해서 'count_lag1,2'를 구현한다.
# Test Data는 별도로 shift()를 활용하여 lag를 진행한다.
X_train_fe['count_lag1']= Y_train_fe.shift(1).values
X_train_fe['count_lag1'].fillna(method = 'bfill',inplace = True)
X_train_fe['count_lag2']= Y_train_fe.shift(2).values
X_train_fe['count_lag2'].fillna(method = 'bfill',inplace = True)
X_train_fe['count_lag2']
X_test_fe['count_lag1']= Y_test_fe.shift(1).values
X_test_fe['count_lag1'].fillna(method = 'bfill',inplace = True)
X_test_fe['count_lag2']= Y_test_fe.shift(2).values
X_test_fe['count_lag2'].fillna(method = 'bfill',inplace = True)
X_test_fe['count_lag2']
현실적인 데이터 전처리 반영한 데이터의 검증 지표
# Data Loading
# location = 'https://raw.githubusercontent.com/cheonbi/DataScience/master/Data/Bike_Sharing_Demand_Full.csv'
location = './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
raw_all = pd.read_csv(location)
# Feature Engineering
raw_fe = feature_engineering(raw_all)
### Reality ###
target = ['count_trend', 'count_seasonal', 'count_Day', 'count_Week', 'count_diff']
raw_feR = feature_engineering_year_duplicated(raw_fe, target)
###############
# Data Split
# Confirm of input and output
Y_colname = ['count']
X_remove = ['datetime', 'DateTime', 'temp_group', 'casual', 'registered']
X_colname = [x for x in raw_fe.columns if x not in Y_colname+X_remove]
X_train_feR, X_test_feR, Y_train_feR, Y_test_feR = datasplit_ts(raw_feR, Y_colname, X_colname, '2012-07-01')
### Reality ###
target = ['count_lag1', 'count_lag2']
X_test_feR = feature_engineering_lag_modified(Y_test_feR, X_test_feR, target)
###############
# Applying Base Model
fit_reg1_feR = sm.OLS(Y_train_feR, X_train_feR).fit()
display(fit_reg1_feR.summary())
pred_tr_reg1_feR = fit_reg1_feR.predict(X_train_feR).values
pred_te_reg1_feR = fit_reg1_feR.predict(X_test_feR).values
# Evaluation
Score_reg1_feR, Resid_tr_reg1_feR, Resid_te_reg1_feR = evaluation_trte(Y_train_feR, pred_tr_reg1_feR,
Y_test_feR, pred_te_reg1_feR, graph_on=True)
display(Score_reg1_feR)
# Error Analysis
error_analysis(Resid_tr_reg1_feR, ['Error'], X_train_feR, graph_on=True)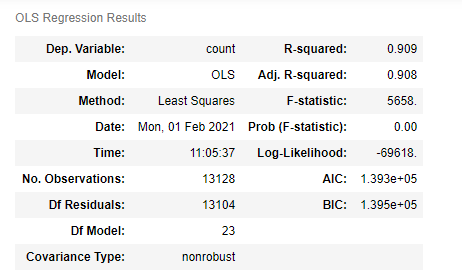


바로 이전의 실습과는 다르게 R-squared 수치가 0.909로 되었다. F-statistic은 유의하다고 나왔으며, 각 column들의 p-value도 이전에는 2개의 column만 유의했다고 결론지어진 반면, 여기에서는 24개 중 15개의 column이 유의하다고 나왔다. Kurtosis도 13000 -> 17로 현격하게 감소하였다. Durbin-Watson지표도 훨씬 적합하게 지표가 나왔다.
Reference : 패스트 캠퍼스 파이썬을 활용한 시계열 분석 A-Z
'딥러닝 > 시계열' 카테고리의 다른 글
| [논문 Review] 콜센터 인입 콜량 예측을 위한 시계열 모델 비교 분석 2 (0) | 2021.03.13 |
|---|---|
| [논문 Review] 콜센터 인입 콜량 예측을 위한 시계열 모델 비교 분석 1 (0) | 2021.03.12 |
| 시계열 분석 실습 코드 - 6 ( OLS, 검증 지표) (0) | 2021.03.04 |
| 시계열 분석 실습 코드 - 5 (시각화, 상관도) (0) | 2021.03.04 |
| 시계열 분석 실습 코드 - 4 (0) | 2021.02.19 |

최근댓글