이번에는 Y의 실제값과, 알고리즘을 통해서 예측한 Y값을 비교함으로써, MAE, MSE, MAPE 등을 계산하고, 시각화하는 실습을 진행한다.
Y의 예측값을 산출하기 위해서는 일단 간단한 데이터 분석 알고리즘이 있어야 한다. 선형회귀 분석의 기초인 OLS를 그 예시로 활용할 계획이다. 일단 OLS에 대해서 간단하게 알아보자.
OLS (Ordianry Least Square)
우리말로는 최소자승법 혹은 최소제곱법이라고 불리기도 한다. OLS는 잔차제곱합인 RSS (Residual Sum of Squares)를 최소화하는 가중치 벡터를 구하는 방법이다.
입력된 데이터를 X라고 하고, 가중치 벡터를 w라고 할 때,
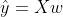
잔차 : (실제 y값) - ( 예측한 y값)
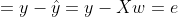
여기에서 잊지말아야 할 점은, e가 상수가 아니라 각 행마다의 잔차를 기록한 벡터라는 것이다.
이것으로 인해서 잔차제곱합 RSS는


이렇게 표현할 수 있다.
잔차의 최소를 구하기 위해 잔차제곱합의 그레디언트 벡터를 구하면
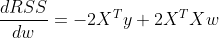
잔차가 최소가 되는 최적화 조건은 해당 식의 값이 0이 되는 지점이다. 이것을 이용해서 식을 다시 한번 정리하면,

여기에서 w^*는 최적 가중치 벡터를 의미한다.
이러한 방식으로 잔차가 최소가 되는 가중치들을 구하는 방식을 최소 제곱법 OLS라고 부른다.
검증지표
위에서는 수학적으로 OLS에 대해서 알아봤지만, 실제 코딩을 하는 경우에는 statsmodels.api를 통해서 간단하게 구현할 OLS를 사용할 수 있다.
fit_reg1 = sm.OLS(Y_train, X_train).fit()
fit_reg1.summary()


.fit( ) 을 통해서 OLS로 학습하여 분석한 결과에 대한 통계적인 수치들을 반환해준다.
여러가지 수치들이 있지만, 지금 간단하게 확인해 볼 것은
첫번째 표에서는 오른쪽 가장 위에 있는 R-squared 수치이다.
R-squared는 결정계수라고 부르며, 회귀 모델에서 독립변수(X)가 종속변수(Y)를 얼마나 잘 설명하는지에 관한 수치이다. 0 ~ 1의 값을 가지고 있으며, 해당 수치만큼 독립변수가 종속변수를 설명할 수 있다고 이해하면 쉽다. R-squared 수치가 1.0이라는 것은 단순히 예측을 잘하는 수준을 넘어서서 과적합(Overfitting)되어있다는 것을 보여준다.
두번째 표에서 각 Column의 p-value는 유의수준(여기에서는 0.05를 유의수준으로 정했다.)보다 커지면, Y를 예측하는 데에 상관성이 적은 특성으로 간주하고, p-value가 유의수준보다 작으면 Y를 에측하는 데에 상관성이 있는 특성으로 간주한다.
세번째 표에 있는 Durbin-Watson (자기상관), Jarque-Bera(JB) (정규분포), Skew (왜도), Kurtosis (첨도) 수치는 잔차들의 특성을 보여준다.
# precision comparisions
pd.concat([Y_train, pd.DataFrame(pred_tr_reg1, index=Y_train.index, columns=['prediction'])], axis=1).plot(kind='line', figsize=(20,6),
xlim=(Y_train.index.min(),Y_train.index.max()),
linewidth=0.5, fontsize=20)
plt.title('Time Series of Target', fontsize=20)
plt.xlabel('Index', fontsize=15)
plt.ylabel('Target Value', fontsize=15)
plt.show()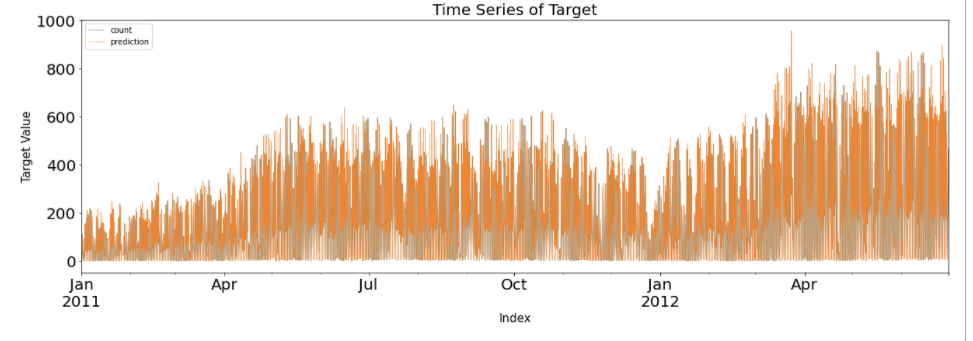
Y의 실제값과 Y의 예측 값을 하나로 겹쳐 그린 그래프이다. 실제값은 파란색 선으로, 예측값은 주황색 선으로 표시가 되어있다. 하지만, 정작 파란색 선은 주황색 선에 겹쳐져 거의 보이지 않고 어렴풋이 보이기만 한다. 이것은 그만큼 예측이 잘 맞는다는 것을 의미하지만, 반대로 너무 Overfitting되어 있는 상태를 보여준다.
이것을 수치적으로 확인해보기 위해서 검증 지표를 사용한다. MAP, MSE, MAPE를 사용하는데,
- MAE : Mean Absolute Error로 모델의 예측값과 실제값의 차이를 더한 수치이다.
- MSE : Mean Square Error로 모델의 예측값과 실제값의 차이의 제곱을 더한 수치이다.
- MAPE : Mean Absolute Percentage Error로 MAE를 퍼센트로 변환한 것이다.
MAE = abs(Y_train.values.flatten() - pred_tr_reg1).mean()
MSE = ((Y_train.values.flatten() - pred_tr_reg1)**2).mean()
MAPE = (abs(Y_train.values.flatten() - pred_tr_reg1)/Y_train.values.flatten()*100).mean()
pd.DataFrame([MAE, MSE, MAPE], index=['MAE', 'MSE', 'MAPE'], columns=['Score']).T
잔차들의 실제값, 제곱한 값을 다 더한 값이라고 보기에는 수치가 비정상적으로 적은 것을 확인할 수 있다.
함수화
def evaluation(Y_real, Y_pred, graph_on = False):
loss_length = len(Y_real.values.flatten()) - len(Y_pred)
if loss_length != 0:
Y_real = Y_real[loss_length:]
if graph_on == True:
pd.concat([Y_real, pd.DataFrame(Y_pred, index = Y_real.index, columns = ['prediction'])], axis = 1).plot(kind = 'line', figsize = (20, 6),
xlim = (Y_real.index.min(), Y_real.index.max()),
linewidth = 3, fontsize = 20)
plt.title('Time Series of Target', fontsize = 20)
plt.xlabel('Index', fontsize = 15)
plt.ylabel('Target Value', fontsize = 15)
MAE = abs(Y_real.values.flatten() - Y_pred).mean()
MSE = ((Y_real.values.flatten() - Y_pred)**2).mean()
MAPE = (abs(Y_real.values.flatten() - Y_pred) / Y_real.values.flatten() * 100).mean()
Score = pd.DataFrame([MAE, MSE, MAPE], index = ['MAE','MSE' ,'MAPE'], columns = ['Score']).T
Residual = pd.DataFrame(Y_real.values.flatten() - Y_pred, index = Y_real.index, columns = ['Error'])
return Score, Residualdef evaluation_trte(Y_real_tr, Y_pred_tr, Y_real_te, Y_pred_te, graph_on = False):
Score_tr, Residual_tr = evaluation(Y_real_tr, Y_pred_tr, graph_on = graph_on)
Score_te, Residual_te = evaluation(Y_real_te, Y_pred_te, graph_on = graph_on)
Score_trte = pd.concat([Score_tr, Score_te], axis = 0)
Score_trte.index = ['Train', 'Test']
return Score_trte, Residual_tr, Residual_te제작한 함수를 이용하여 시각화와 검증지표를 계산해보자.
Score_reg1, Resid_tr_reg1, Resid_te_reg1 = evaluation_trte(Y_train, pred_tr_reg1, Y_test, pred_te_reg1, graph_on=True)
Score_reg1
Reference :
4.2 선형회귀분석의 기초 — 데이터 사이언스 스쿨
회귀분석은 독립변수 \(x\)에 대응하는 종속변수 \(y\)와 가장 비슷한 값 \(\hat{y}\)를 출력하는 함수 \(f(x)\)를 찾는 과정이다. 만약 \(f(x)\)가 다음과 같은 선형함수면 이 함수를 **선형회귀모형(linear
datascienceschool.net
패스트 캠퍼스 파이썬을 활용한 시계열 분석 A-Z
'딥러닝 > 시계열' 카테고리의 다른 글
| [논문 Review] 콜센터 인입 콜량 예측을 위한 시계열 모델 비교 분석 1 (0) | 2021.03.12 |
|---|---|
| 현실적인 데이터 전처리 (0) | 2021.03.05 |
| 시계열 분석 실습 코드 - 5 (시각화, 상관도) (0) | 2021.03.04 |
| 시계열 분석 실습 코드 - 4 (0) | 2021.02.19 |
| 시계열 분석 실습 코드 - 3 (0) | 2021.02.18 |

최근댓글