데이터 셋 : https://www.kaggle.com/c/bike-sharing-demand/data 에서 train.csv파일을 bike_train.csv로 저장한 뒤 실습을 진행한다.
데이터 셋의 피처들을 확인하면
- datatime : 날짜
- season : 1 = 봄, 2 = 여름, 3 = 가을, 4 = 겨울
- holiday : 1 = 주말 및 휴일, 0 = 평일
- workingday: 1 = 주중, 0 = 주말 및 휴일
- weather : 1 = 맑음, 약간 구름 낀 흐림, 2 = 안개, 안개 + 흐림, 3 = 가벼운 눈, 가벼운 비 + 천둥, 4 = 심한 눈/비, 천둥/번개
- temp : 온도(섭씨)
- atem : 체감 온도(섭씨)
- humidity : 상대 습도
- windspeed : 풍속
- casual : 미등록 사용자 대여수
- registered : 등록된 사용자 대여수
- count : 대여 횟수(casual + registered)
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings("ignore", category = RuntimeWarning)
bike_df = pd.read_csv("bike_train.csv")
print(bike_df.shape)
bike_df.head()필요한 라이브러리들을 import 하고 bike_train.csv 파일을 DataFrame 데이터형으로 만들어서 어떻게 되어있는지 확인한다.
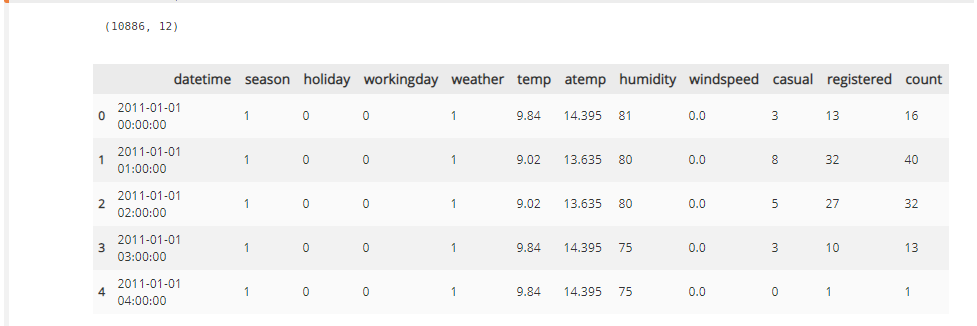
bike_df.info()
각 칼럼들의 데이터 타입을 확인하고 NaN 값이 존재하는지 확인한다.
(간략하게 널값이 있는지 없는지 확인하는 것이고, 이후에 조금 더 세밀하게 확인할 필요가 있다. )
datetime
bike_df.info()를 통해서 피처들의 데이터 타입을 확인해 보면 'datetime' 피처를 제외하고는 모두 숫자형 데이터인것을 확인할 수 있다. datetime은 날짜와 시간을 표시하고 있는 string 데이터 타입을 가진 피처이다.
데이터 가공을 쉽게 하기 위해서 string으로 되어 있는 데이터를 datetime 데이터 형으로 전환한다.
# 문자열을 datetime 타입으로 변경
bike_df['datetime'] = bike_df.datetime.apply(pd.to_datetime)
# datetime 타입에서 년, 월, 일, 시간 추출
bike_df['year'] = bike_df.datetime.apply(lambda x : x.year)
bike_df['month'] = bike_df.datetime.apply(lambda x : x.month)
bike_df['day'] = bike_df.datetime.apply(lambda x : x.day)
bike_df['hour'] = bike_df.datetime.apply(lambda x : x.hour)
bike_df.head(3)pd.to_datetime의 함수를 통해서 datetime 데이터 형으로 전환되고, 이 데이터 타입을 이용해서 쉽게 년,월,일,시의 정보를 추출할 수 있다.

필요없는 피처 삭제하기
위에서 datetime 칼럼을 통해서 년, 월, 일, 시의 정보를 별도의 피처로 만들어 데이터 프레임에 추가하였으므로 datetime 피처는 더이상 필요하지 않다. 또한, casual과 registered 두 피처를 더하면 label data인 count이기 때문에, 학습할 때 이 두 피처를 포함하는 것은 오히려 학습 모델이 Overfitting되도록 한다. 그래서 datetime, casual, registered 세가지의 피처를 삭제한다.
drop_columns = ['datetime', 'casual', 'registered']
bike_df.drop(drop_columns, axis = 1, inplace = True)
평가지표
캐글에서 요구한 성능 평가 방법은 RMSLE(Root Mean Squared Log Error)이다.

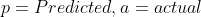
여기에서 log 안에 +1을 해주는 이유는 p나 a의 값이 0일 때 음의 무한대여서 언더플로우가 발생하는 것을 방지하기 위함이다.
RMSLE의 장점 :
- 아웃라이어가 있더라도 크게 영향을 받지 않는다.
- 상대적 Error를 측정
- Under Estimation에 큰 페널티를 부여
사이킷런에서는 RMSLE를 제공하지 않아 함수를 직접 만들어야 한다.
from sklearn.metrics import mean_squared_error, mean_absolute_error
# log 값 변환 시 NaN 등의 이슈로 log()가 아닌 log1p()를 이용해 RMSLE 계산
def rmsle(y, pred):
log_y = np.log1p(y)
log_pred = np.log1p(pred)
squared_error = (log_y - log_pred)**2
rmsle = np.sqrt(np.mean(squared_error))
return rmsle
def rmse(y, pred):
return np.sqrt(mean_squared_error(y, pred))
#MSE, RMSE, RMSLE를 모두 계산
def evaluate_regr(y, pred):
rmsle_val = rmsle(y, pred)
rmse_val = rmse(y, pred)
#MAE는 사이킷런의 mean_absolute_error()로 계산
mae_val = mean_absolute_error(y, pred)
print("RMSLE: {0:.3f}, RMSE : {1:.3f}, MAE : {2:.3f}".format(rmsle_val, rmse_val, mae_val))마지막 evaluate_regr은 RMSLE, RMSE, MAE를 한꺼번에 출력하는 함수이다.
타깃 데이터의 로그 변환
회귀 모델을 적용하기 전에 데이터 세트에 대해서 먼저 처리해야 할 사항 2가지
- 결괏값(타깃 데이터)이 정규 분포로 되어 있는가?
- 카테고리형 데이터 셋을 One-Hot Encoding을 수행하였는가?
먼저 Linear Regression 모델을 통해서 회귀 예측을 하면
from sklearn.model_selection import train_test_split, GridSearchCV
from sklearn.linear_model import LinearRegression, Ridge, Lasso
y_target = bike_df['count']
X_features = bike_df.drop(['count'], axis = 1, inplace = False)
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target, test_size = 0.3, random_state = 0)
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
pred = lr_reg.predict(X_test)
evaluate_regr(y_test, pred)이렇게 모델을 학습하여 예측했을 때, 평가지표는 RMSLE: 1.165, RMSE : 140.900, MAE : 105.924로 나오게 된다.
이 평가 지표는 예측 오류로서는 큰 값이므로, 현재 데이터가 제대로 전처리되지 않은 부분이 존재한다는 것을 시사한다.
실제 값과 예측 값의 차이가 가장 큰 데이터 5개를 확인하는 코드를 짜보자.
# 실제값과 예측 값이 어느 정도 차이가 나는지 DF의 칼럼으로 만들어서 오류 값이 가장 큰 순으로 5개 확인
def get_top_error_data(y_test, pred, n_tops = 5):
#DF의 칼럼으로 실제 대여 횟수(Count)와 예측값을 서로 비교할 수 있도록 생성.
result_df = pd.DataFrame(y_test.values, columns = ['real_count'])
result_df['predicted_count'] = np.round(pred)
result_df['diff'] = np.abs(result_df['real_count'] - result_df['predicted_count'])
#예측값과 실제 값이 가장 큰 데이터 순으로 출력
print(result_df.sort_values('diff', ascending = False)[:n_tops])
get_top_error_data(y_test, pred, n_tops = 5)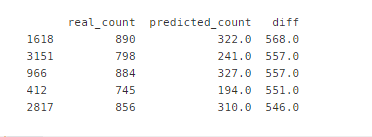
실제 자전거 대여 횟수와 예측 자전거 대여 횟수가 500회 이상 차이가 나는 것을 통해서 예측 오류가 크다는 것을 확인할 수 있다. 이렇게 큰 예측 오류가 발생한다면 가장 먼저 살펴볼 것은 타깃값의 분포가 정규 분포를 따르고 있는지 확인하는 것이다.
타깃 데이터의 분포를 확인해보자.
y_target.hist()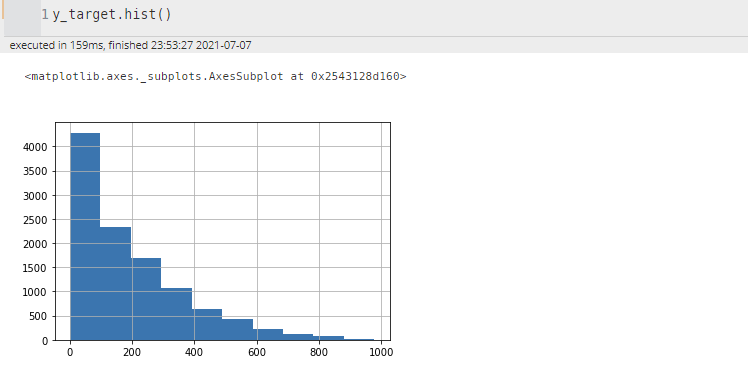
0 ~ 200 사이에 타깃 데이터가 몰려 있는 것을 확인할 수 있다. 이렇게 한쪽으로 쏠려 있는 분포를 나타내고 있는 경우에는 로그 변환을 통해서 정규 분포와 비슷한 형태로 변환할 수 있다.
y_log_transform = np.log1p(y_target)
y_log_transform.hist()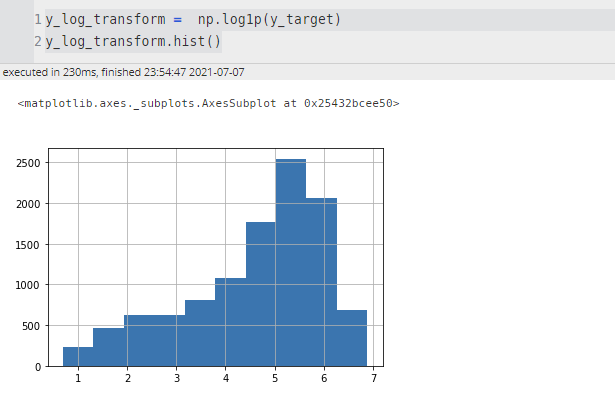
(np.log1p() 함수를 사용한 것은 0인 데이터의 경우 언더플로우 문제가 발생할 수 있기 때문이다.)
이렇게 타깃 데이터를 변환한 후에 다시 평가를 수행해보자.
# 타깃 칼럼인 count 값을 log1p로 로그 변환
y_target_log = np.log1p(y_target)
#로그 변환된 y_target_log를 반영해 학습/ 테스트 데이터 세트 분할
X_train, X_test, y_train, y_test = train_test_split(X_features, y_target_log, test_size = 0.3, random_state = 0)
lr_reg = LinearRegression()
lr_reg.fit(X_train, y_train)
pred = lr_reg.predict(X_test)
#테스트 데이터 세트의 Target 값은 로그 변환됐으므로 다시 expm1을 이용해 원래 스케일로 변환
y_test_exp = np.expm1(y_test)
# 예측값 역시 로그 변환된 타깃 기반으로 학습돼 예측됐으므로, 다시 expm1로 스케일 변환
pred_exp = np.expm1(pred)
evaluate_regr(y_test_exp, pred_exp)타깃 데이터와 예측값 모두 로그 변환이 되어 있는 상태이므로, 예측까지 진행한 후에 평가 지표를 계산하기 위해서는 다시 np.expm1() 함수를 통해서 실제 값으로 변환해주어야 한다.
평가 지표를 확인해보면, RMSLE: 1.017, RMSE : 162.594, MAE : 109.286 이 나오게 된다.
적절한 조치를 취해 주었지만, 성능 지표가 좋아지지 않거나, 오히려 더 낮은 성능을 보이는 경우가 있다. 이런 경우에는 해당 전처리 과정이 잘못되었을 수도 있지만, 다른 전처리 과정이 추가적으로 필요한 경우도 있다.
One-Hot Encoding
선형 회귀 모델이 학습의 과정을 거쳐 각 피처에 대한 계수를 산출했을 때, 해당 계수가 크다면, 그만큼 결과에 큰 영향을 끼치는 피처라는 것을 의미한다.
따라서, 각 피처의 회귀 계수 값을 시각화해보자.
coef = pd.Series(lr_reg.coef_, index = X_features.columns)
coef_sort = coef.sort_values(ascending = False)
sns.barplot(x= coef_sort.values, y = coef_sort.index)
Year 피처의 회귀 계수 값이 독보적으로 큰 계수 값을 가지고 있다.
하지만 연도에 따라서 자전거 대여 횟수가 크게 영향을 받는다는 것은 논리에 맞지 않는다.
이렇게 많은 영향을 받는 이유는 year 피처는 연도를 뜻하므로 카테고리 형 피처지만 숫자형 값으로 되어있다. 이처럼 숫자형 카테고리 값을 선형 회귀에 사용할 경우 회귀 계수를 연산할 때 이 숫자형 값에 크게 영향을 받는 경우가 발생할 수 있다. 이런 경우에는 원-핫 인코딩을 적용해 변환한다.
각 피처의 의미를 이해해야 적절한 전처리 과정을 판단할 수 있다.
# 'year' ,'month','day','hour' 등의 피처를 One-Hot Encoding
X_features_ohe = pd.get_dummies(X_features, columns = ['year','month','day','hour','holiday','workingday','season','weather'])#원-핫 인코딩이 적용된 피처 데이터 세트 기반으로 학습/예측 데이터 분할
X_train, X_test, y_train, y_test = train_test_split(X_features_ohe, y_target_log, test_size = 0.3, random_state = 0)
#모델과 학습/ 테스트 데이터 세트를 입력하면 성능 평가 수치를 반환
def get_model_predict(model, X_train, X_test, y_train, y_test, is_expm1=False):
model.fit(X_train, y_train)
pred = model.predict(X_test)
if is_expm1 :
y_test = np.expm1(y_test)
pred = np.expm1(pred)
print("###", model.__class__.__name__, '###')
evaluate_regr(y_test, pred)
#end of function get_model_predict
# 모델별로 평가 수행
lr_reg = LinearRegression()
ridge_reg = Ridge(alpha = 10)
lasso_reg = Lasso(alpha = 0.01)
for model in [lr_reg, ridge_reg, lasso_reg]:
get_model_predict(model, X_train, X_test, y_train, y_test, is_expm1=True)
One-Hot Encoding을 수행한 결과 예측 오류가 2/3정도로 줄어든 것을 확인할 수 있다. 이번에는 어떤 피처가 예측 결과에 큰 영향을 주는지 계수 값이 큰 피처 상위 25개를 선별하여 시각화해보자.
coef = pd.Series(lr_reg.coef_, index = X_features_ohe.columns)
coef_sort = coef.sort_values(ascending= False)[:25]
sns.barplot(x = coef_sort.values, y = coef_sort.index)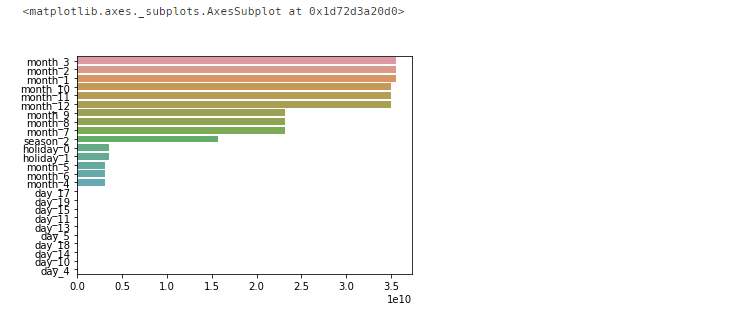
회귀 트리 모델을 이용하여 예측
from sklearn.ensemble import RandomForestRegressor, GradientBoostingRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
# 랜덤 포레스트, GBM, XGBoost, LightGBM model 별로 평가 수행
rf_reg = RandomForestRegressor(n_estimators = 500)
gbm_reg = GradientBoostingRegressor(n_estimators = 500)
xgb_reg = XGBRegressor(n_estimators = 500)
lgbm_reg = LGBMRegressor(n_estimators = 500)
for model in [rf_reg, gbm_reg, xgb_reg, lgbm_reg]:
# XGBoost의 경우 DF이 입력될 경우 버전에 따라 오류 발생 가능. ndarray로 변환
get_model_predict(model, X_train.values, X_test.values, y_train.values, y_test.values, is_expm1= True)이전에 배웠던 여러가지 회귀 트리 모델들을 이용해서 학습 및 예측을 수행한 후에 성능 지표를 확인해보자.

One-Hot Encoding을 수행한 후 예측했을 때보다 오류가 절반정도로 줄어든 것을 확인할 수 있다. 하지만, 항상 회귀 트리 모델이 선형 회귀 모델보다 더 좋은 성능을 낸다는 것을 보장하지는 않는다. 데이터에 따라서 더 좋은 성능을 보이는 모델이 다르므로, 실제 데이터 분석을 하는 경우에는 많은 모델들을 사용하여 학습 및 예측을 수행하고 성능을 비교해야 한다.
reference :파이썬 머신러닝 완벽 가이드
https://bkshin.tistory.com/entry/머신러닝-17-회귀-평가-지표
머신러닝 - 17. 회귀 평가 지표
회귀의 평가를 위한 지표는 실제 값과 회귀 예측값의 차이를 기반으로 합니다. 회귀 평가지표 MAE, MSE, RMSE, MSLE, RMSLE는 값이 작을수록 회귀 성능이 좋은 것입니다. 값이 작을수록 예측값과 실제값
bkshin.tistory.com
RMSLE (Root Mean Squared Log Error)
회귀의 평가를 위한 지표는 실제 값과 회귀 예측값의 차이를 기반으로 합니다. 회귀 평가지표 중에 RMSLE가 있는데 값이 작을수록 회귀 성능이 좋은 것입니다. 예측값과 실제값의 차이가 없다는
ahnjg.tistory.com
'기계학습 > Machine Learning' 카테고리의 다른 글
| Linear Regression - Gradient Descent란? (0) | 2021.07.22 |
|---|---|
| Machine Learning- 회귀 (0) | 2021.07.22 |
| [파이썬 머신러닝 완벽 가이드] 전처리, 로지스틱 회귀, 회귀 트리 (0) | 2021.07.08 |
| [파이썬 머신러닝 완벽가이드] - 규제선형 모델 : 릿지, 라쏘 엘라스틱넷 (0) | 2020.09.15 |
| [파이썬 머신러닝 완벽 가이드] : 다항 회귀 ( Polynomial, 편향, 분산) (0) | 2020.09.02 |

최근댓글