SVM이란 분류 모델로 Hyper plane이라는 선 혹은 평면이라는 기준을 가지고 분류하는 것이다. SVM은 이 Hyper plane을 구하는 것이고, 즉 w와 b를 구하는 것이 가장 중요하다. 여기서는 선형 SVM을 다루고 다음 페이지에서 비선형 SVM을 다루고자 한다.
SVM에서 class를 나누는 기준은?
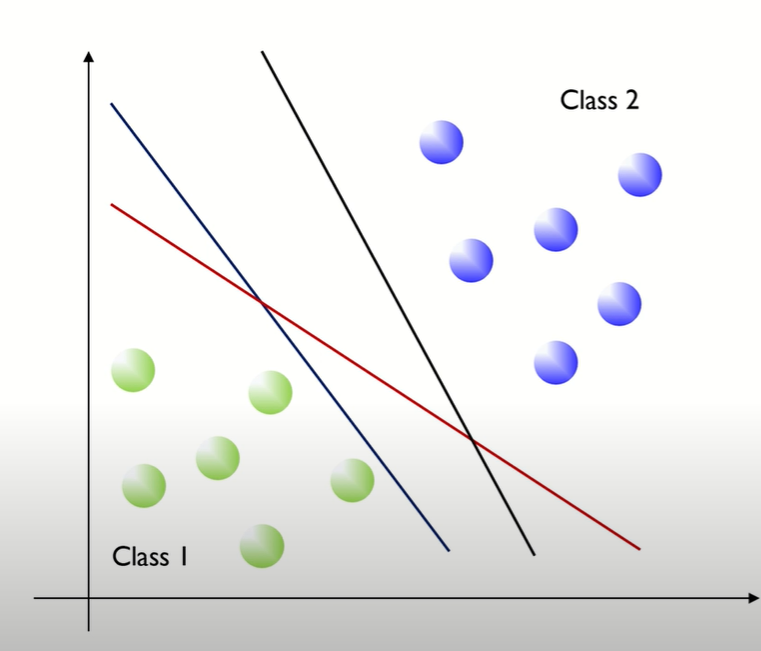
위 사진을 보면 두 class를 나누는 hyperplane(여기서는 직선)이 무한이 많다. 그렇다면 어떤 hyperplane이 가장 좋은 hyperplane이고, 좋다는 것의 기준은 무엇일까?
좋다는 것의 기준이자 SVM의 목표는 training data의 margin이 최대화 되는 것을 찾는 것이다. 즉 margin을 최대화 한다는 것은 일반적인 error를 최소화 한다는 것이고, 이는 좋은 예측 성능을 나타낸다.
그렇다면 마진은?
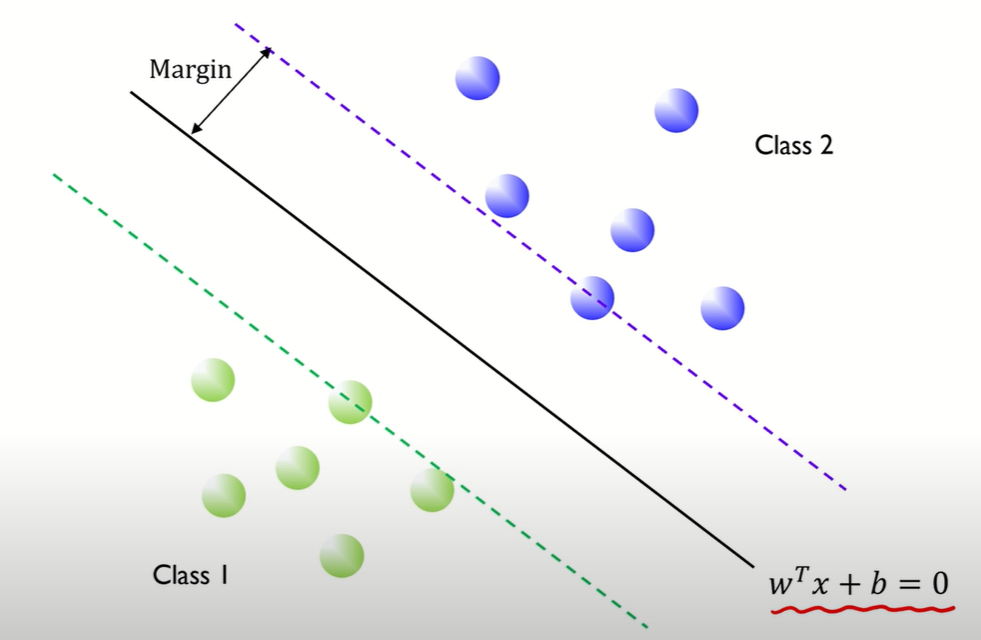
Margin은 각 클래스에서 가장 가까운 관측치 사이의 거리이다. 위 그림에서는 파란색 원이 hyperplane(wTx+b)와 가장 가까이 있고, 이 거리를 Margin이라고 부른다. 또한 Margin은 w(기울기)로 표현 가능하다.
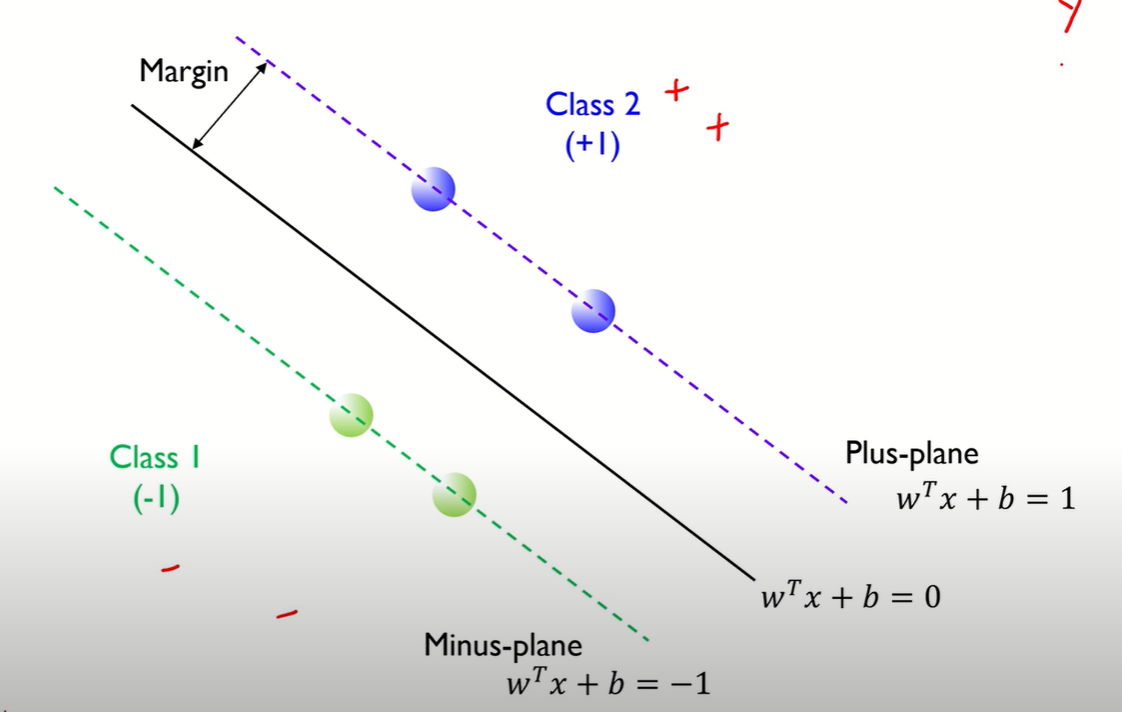
이 Margin을 최대화하는 hyper plane을 찾았으면 class는 hyperplane이 >=1일 때 class2(+1)이 되고 <=-1일 때 class 1이 되면서 최종적으로 분류가 된다.
SVM의 수식화

수식을 정리하면 람다 같은 2/w의 제곱이 되고 이 람다를 통해 최종적으로 Margin이 2/||w||2라는 것을 알 수 있다. ||w||2를 구하는 방법은 아래 L2 norm을 통해 구할 수 있다.

이렇게 최종으로 나온 수식을 바탕으로 margin을 최대화하는 w와 b를 찾는 것이다. 이는 다시 역수를 취해서 최소화하는 문제로 풀 수 있고 L2 norm으로 w 계산상의 편의를 위해, 제곱을 한다.
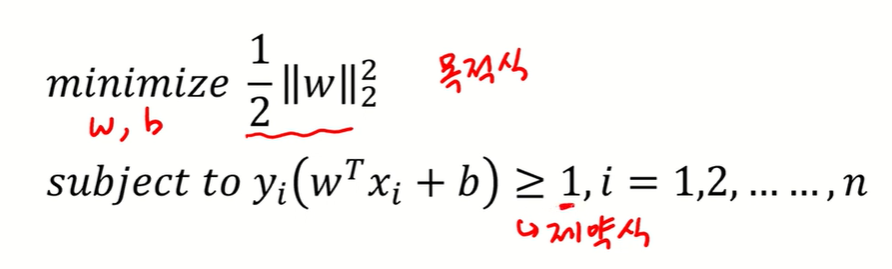
정리하자면 SVM은 위와 같은 목적식과 제약식이 있다. 목적식은 선형회귀에서 cost function이라고 보면 된다. 이 값을 최소화하는 것이 목적이고, 제약식은 hyper plane을 통해 training data를 완벽하게 separating하는 조건을 뜻한다. 여기서 목적식은 quadratic이고 constraint는 linear해서 quadratic programming(2차식이라고 생각하면 된다)으로 풀 수 있다. quadratic programming은 convex optimization이고 이는 전역 최적해가 존재해서 문제를 풀 수 있다.
Lagrangian Formulation
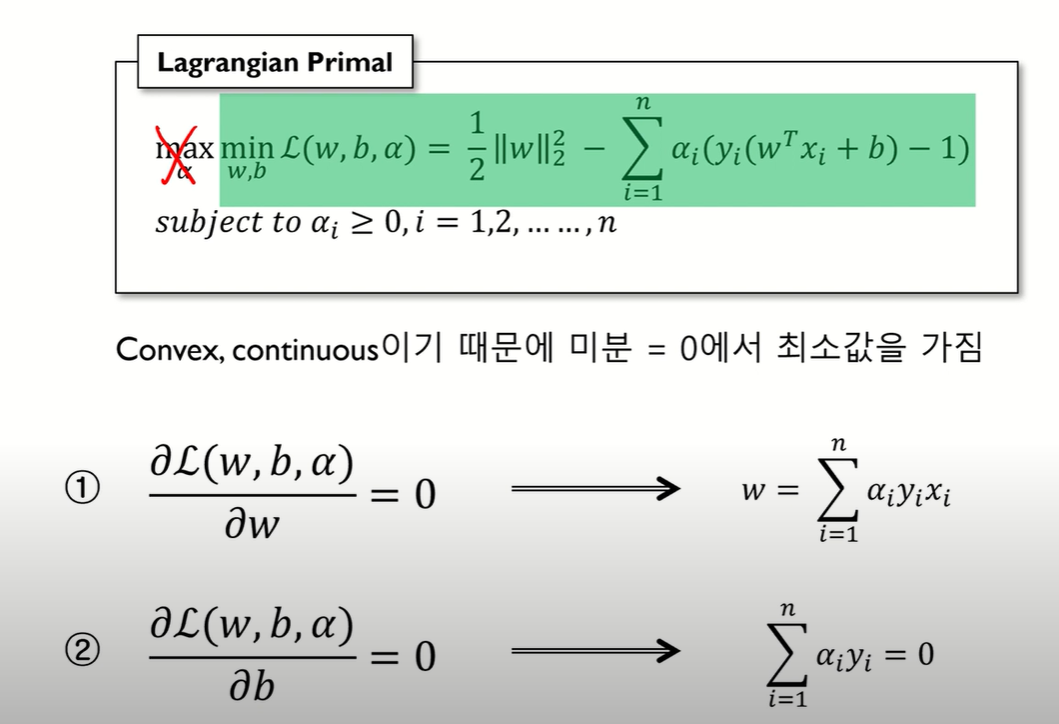
위 목적식과 제약식을 바탕으로 Lagrangian Primal을 구할 수 있고, 이 식을 각각 w와 b로 편미분해서 a값을 구할 수 있다. 이 a값을 구해야 나중에 w와 b를 구할 수 있다.
Lagrangian Dual

Lagrangian Formulation을 더 간단하게 계산상의 편의를 위해 Dual문제로 풀 수 있다. 이는 똑같이 quadratic이라서 전역최적해가 존재하고, a값을 구하는 것이 핵심이고 이에 대한 solution을 위 식에서 얻을 수 있다.

KKT 컨디션은 위에서 말한 (w,b,a)가 Lagrangian dual problem의 최적해가 되기 위한 조건을 뜻한다. 위 4가지 조건을 연산하여 w,b,a를 구할 수 있다.

solution을 구하는 방법을 기하학적으로 설명하면 위와 같다. ai가 >0일 때, =0일 때도 나눠서 풀 수 있는데 먼저 1번인 ai>0일 때는 yi(wTxi+b)=1이 되어 margin위에 존재한다. 즉 support vector를 말한다. 2번인 ai=0일 때는 yi(~~)!=0이기 때문에 마진 위에 있지 않고 경계 밖에 있는 것을 말한다.

즉 정리하자면 xi가 support vector인 경우에만 ai>=0이므로 위 식이 성립한다. 위 support vector만을 이용하여 최적의 hyperplane(w와 b)을 구할 수 있다.

이렇게 구한 hyperplane을 바탕으로 새로운 데이터가 들어왔을 때, hyperplane보다 아래 있으면 class1으로 예측하고 위에 있으면 class2로 예측한다.
출처 : 김성범 인공지능공학연구소 핵심 머신러닝 강의(SVM)
'기계학습 > Machine Learning' 카테고리의 다른 글
| [DATA/AI직무 면접 대비] ML&DL 관련 개념 한 줄 정리 (0) | 2022.10.24 |
|---|---|
| [DATA/AI직무 면접 대비] 데이터사이언스&ML 관련 용어 한 줄 정리 (0) | 2022.10.24 |
| Feature Scaling이란? (0) | 2021.07.23 |
| Multivariate Linear Regression이란? (0) | 2021.07.22 |
| Linear Regression - Gradient Descent란? (0) | 2021.07.22 |

최근댓글